题目内容
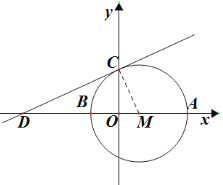
【题目】如图,在直角坐标系中,以点![]() (3,0)为圆心,以6为半径的圆分别交
(3,0)为圆心,以6为半径的圆分别交![]() 轴的正半轴于点
轴的正半轴于点![]() ,交
,交![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 轴的负半轴于点
轴的负半轴于点![]() (-9,0)
(-9,0)
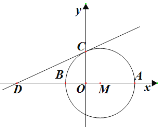
(1)求![]() 两点的坐标;
两点的坐标;
(2)若抛物线![]() 经过
经过![]() 、
、![]() 两点,求此抛物线的解析式;
两点,求此抛物线的解析式;
(3)求证:直线![]() 是⊙
是⊙![]() 的切线;
的切线;
【答案】(1)A(9,0),C(0,3![]() );(2)
);(2)![]() ;(3)见解析
;(3)见解析
【解析】
对(1),已知了圆心M的坐标,即可得出OM的长,题中也告诉了圆的半径即可得出OA的长也就能求出A点的坐标.求C点坐标就是求OC的长,可连接MC,在直角三角形OMC中用勾股定理即可求出OC的长;
对(2),运用待定系数法,将M、A的坐标代入抛物线中即可求出其解析式.
对(3),本题只需证MC⊥CD即可,在直角三角形OCD中,根据OD和CD的长即可求出∠CDO的度数,在直角三角形MCO中可求出∠CMO的度数,有这两个角的度数即可求出∠DCM=90°,由此可得证;
解:(1)∵![]()
∴![]()
∴![]()
∴![]()
连接CM,
在Rt△OCM中,∵![]()
∴![]()
(2)把![]() ,
,![]() 代入
代入![]() 得:
得:
![]()
解得![]()
∴抛物线解析式为![]() .
.
(3)∵![]()
∴OD=9
在Rt△DCO中,∵![]()
∴![]()
∵![]()
∴在△DCM中![]()
∴△DCM是Rt△
∴MC⊥DC于点C
∵MC是半径
∴直线CD是⊙M的切线.

 阅读快车系列答案
阅读快车系列答案【题目】共享单车逐渐成为市民喜爱的“绿色出行” 方式之一,今年国庆假期某一天,济川中学初三数学社团的同学们随机调查了一个社区,将这天部分出行市民使用共享单车的数据整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 这天部分出行市民使用共享单车次数的中位数是__________,众数是__________
(2) 这天部分出行市民平均每人使用共享单车多少次?
(3) 若该社区这天有1500人出行,请你估计这天使用共享单车次数在3次以上(含3 次)的市民有多少人?
【题目】有这样一个问题:探究函数y=![]() 的图象与性质:
的图象与性质:
小宏根据学习函数的经验,对函数y=![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小宏的探究过程,请补充完整:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | … |
y | … | ﹣ | ﹣ | 0 | m |
| ﹣ | ﹣ | 0 |
| n | … |
求m,n的值;
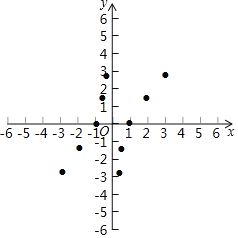
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,写出该函数的性质(两条即可):
①
② .