题目内容
1．已知xyz≠0，且x+3y+z=0，2x+3y-z=0，求$\frac{x+2y-7z}{3x+5y+z}$．分析 把z当作已知数求出x y的值，代入即可求出答案．
解答 解：∵x+3y+5z=0，2x+3y+z=0，xyz≠0，
∴$\left\{\begin{array}{l}{x+3y+z=0①}\\{2x+3y-z=0②}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=2z}\\{y=-z}\end{array}\right.$，
∴$\frac{x+2y-7z}{3x+5y+z}$=$\frac{2z-2z-7z}{6z-5z+z}$=-$\frac{7}{2}$．
点评 此题主要考查了分式的化简求值，正确用同未知数表示出x，y是解题关键．
练习册系列答案
相关题目
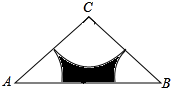如图，在△ABC中，∠C=120°，CA=CB=6，分别以A，B，C为圆心，以3为半径画弧，三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6．
如图，BC是半⊙O的直径，点P是半圆弧的中点，点A是弧BP的中点，AD⊥BC于D，连结AB、PB、AC，BP分别与AD、AC相交于点E、F．