题目内容
20．如果有4个不同的正整数m、n、p、q满足（m-2015）（n-2015）（p-2015）（q-2015）=4，那么m+n+p+q等于8060．分析 根据有理数的乘法运算法则判断出4的算式，然后列式计算即可得解．
解答 解：∵正整数m、n、p、q是4个不同的正整数，
∴（m-2015）（n-2015）（p-2015）（q-2015）=（-1）×1×（-2）×2=4，
∴（m-2015）+（n-2015）+（p-2015）+（q-2015）=-1+1-2+2=0，
∴m+n+p+q=2015×4=8060．
故答案为：8060．
点评 本题考查了有理数的乘法，判断出相乘的积是4的四个因数是解题的关键，也是本题的难点．
练习册系列答案
相关题目
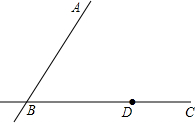已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点，直线DE∥AB，且点E到B，D两点的距离相等．
双曲线y1=$\frac{12}{x}$与y2=$\frac{6}{x}$在第一象限内的图象如图所示，作直线l平行于y轴，与双曲线分别交于A，B两点，连接OA，OB，则△AOB的面积为3．
如图，点A在反比例函数y=$\frac{1}{x}$（x＞0）的图象上，点B在反比例函数y=-$\frac{3}{x}$（x＜0）的图象上，且OA⊥OB．线段AB交反比例函数y=$\frac{1}{x}$（x＞0）的图象于另一点C，连接OC，若点C为AB的中点，则tan∠OCA的值为$\sqrt{3}$．
如图，△ABC中，AB=AC，点D是BC上一点，DE⊥AB于E，FD⊥BC于D，G是FC的中点，连接GD．求证：GD⊥DE．