题目内容
某旅游团计划在3天内游览3个景点A、B、C,每天只能游览其中的1个景点,如果采取抽签的方法决定游览顺序,那么:
(1)共有几种不同的安排方案?
(2)第1天游览景点A,第2天游览景点B,第3天游览景点C的概率是多少?
(3)第1天游览景点A的概率是多少?
(1)共有几种不同的安排方案?
(2)第1天游览景点A,第2天游览景点B,第3天游览景点C的概率是多少?
(3)第1天游览景点A的概率是多少?
考点:列表法与树状图法
专题:
分析:(1)把所有可能的结果一一列举出了即可;
(2)根据(1)中的方案可找到第1天游览景点A,第2天游览景点B,第3天游览景点C的情况,进而可求出其概率;
(3)根据(1)中的方案可得到第1天游览景点A的情况,进而可求出其概率
(2)根据(1)中的方案可找到第1天游览景点A,第2天游览景点B,第3天游览景点C的情况,进而可求出其概率;
(3)根据(1)中的方案可得到第1天游览景点A的情况,进而可求出其概率
解答:解:(1)所有可能的方案有:A,B,C;A,C,B;B,C,A;B,A,C;C,A,B;C,B,A共六种;
(2)由(1)可知第1天游览景点A,第2天游览景点B,第3天游览景点C的情况只有一种,所以其概率为:
;
(3)由(1)可知第1天游览景点A的情况有两种,所以第1天游览景点A的概率为:
=
.
(2)由(1)可知第1天游览景点A,第2天游览景点B,第3天游览景点C的情况只有一种,所以其概率为:
| 1 |
| 6 |
(3)由(1)可知第1天游览景点A的情况有两种,所以第1天游览景点A的概率为:
| 2 |
| 6 |
| 1 |
| 3 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
袋子中装有4个黑球、2个白球,这些球的形状、大小、质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋子中摸出1个球.下面说法正确的是( )
| A、这个球一定是黑球 |
| B、这个球一定是白球 |
| C、“摸出黑球”的可能性大 |
| D、“摸出黑球”和“摸出白球”的可能性一样大 |
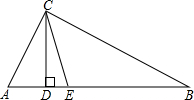 如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )
如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )| A、10° | B、15° |
| C、20° | D、25° |
观察下列式子,正确的是( )
| A、-2(x-3y)=-2x+6y |
| B、a+3>3 |
| C、4÷(2+1)=4÷2+4÷1 |
| D、16y2-7y2=9 |

 如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为
如图,在△ABC中,∠C=90°,AD平分∠BAC,BC=10cm,BD=6cm,则点D到AB的距离为 已知平面直角坐标系中三点的坐标分别为:A(4、4),B(-2,2),C(3,0)
已知平面直角坐标系中三点的坐标分别为:A(4、4),B(-2,2),C(3,0)