题目内容
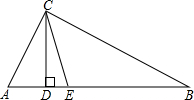 如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )
如图,在△ABC中,∠ACB=90°,CD是斜边上的高,CE是△ABC的角平分线,已知∠B=30°,则∠ECD的角度为( )| A、10° | B、15° |
| C、20° | D、25° |
考点:三角形内角和定理
专题:
分析:先根据直角三角形的性质求出∠B的度数,再由CD⊥AB可知∠ADC=90°,根据直角三角形的性质求出∠ACD的度数,由角平分线的性质求出∠ACE的度数,根据∠DCE=∠ACE-∠ACD即可得出结论.
解答:解:∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=90°-30°=60°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°-60°=30°.
∵CE是△ABC的角平分线,
∴∠ACE=
∠ACB=
×90°=45°,
∴∠DCE=∠ACE-∠ACD=45°-30°=15°.
故选B.
∴∠A=90°-30°=60°.
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=90°-60°=30°.
∵CE是△ABC的角平分线,
∴∠ACE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DCE=∠ACE-∠ACD=45°-30°=15°.
故选B.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
下列合并同类项正确的是( )
| A、2+x=2x | ||
| B、x+x+x=3x | ||
| C、3ab-ab=3 | ||
D、
|
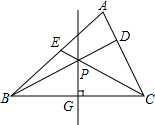 如图,P为△ABC的边BC的垂直平分线上的一点,此垂直平分线交BC于G,且∠PCB=
如图,P为△ABC的边BC的垂直平分线上的一点,此垂直平分线交BC于G,且∠PCB=