题目内容
14.(1)$\sqrt{16}$+$\root{3}{-27}$+3$\sqrt{3}$-$\sqrt{(-3)^{2}}$(2)|1-$\sqrt{2}$|+|$\sqrt{2}$-$\sqrt{3}$|+|$\sqrt{2}$-1|
分析 (1)原式利用平方根及立方根定义计算即可得到结果;
(2)原式利用绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)原式=4-3+3$\sqrt{3}$-3=3$\sqrt{3}$-2;
(2)原式=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{2}$-1=$\sqrt{2}$+$\sqrt{3}$-2.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
4.下列运算正确的是( )
| A. | (-2ab)•(-3ab)3=-54a4b4 | B. | (3.5×105)÷(5×106)=7 | ||
| C. | (-0.16)•(-10b2)3=-b7 | D. | (2×10n)($\frac{1}{2}$×10n)=102n |
9.下列命题中,假命题是( )
| A. | 一组邻边相等的矩形是正方形 | |
| B. | 一组邻边相等的平行四边形是菱形 | |
| C. | 对角线互相平分的四边形是平行四边形 | |
| D. | 有一个角是直角的四边形是矩形 |
19.下列图形:
①正方形;②矩形;③等边三角形;④线段;⑤角;⑥平行四边形,
其中,绕某个点旋转180°能与自身重合的有( )
①正方形;②矩形;③等边三角形;④线段;⑤角;⑥平行四边形,
其中,绕某个点旋转180°能与自身重合的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6. 如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )
如图,在五边形ABCDE中,∠A+∠B+∠E=∠EDC+∠BCD+140°,DF,CF分别平分∠EDC和∠BCD,则∠F的度数为( )| A. | 100° | B. | 90° | C. | 80° | D. | 70° |
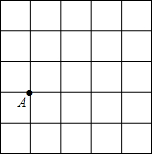 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.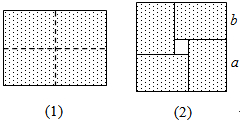 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是(a-b)2.
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是(a-b)2.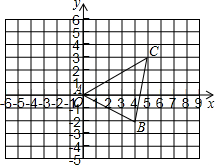 如图A、B、C是△ABC三个顶点
如图A、B、C是△ABC三个顶点