题目内容
在直角三角形ABC中,∠ACB=90°,CD⊥AB,CE为AB边上的中线,且∠BCD=3∠DCA,求证:DE=DC.
考点:直角三角形斜边上的中线,直角三角形的性质
专题:证明题
分析:根据:∠ACB=90°且∠BCD=3∠DCA求得∠BCD和∠DCA的度数,然后根据直角三角形的性质求得∠A、∠B的度数,然后根据三角形的性质证明:∠DCE=∠CED,利用等角对等边即可证得.
解答: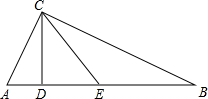 解:∵∠ACB=90°且∠BCD=3∠DCA,
解:∵∠ACB=90°且∠BCD=3∠DCA,
∴∠ACD=90°×
=22.5°,∠BCD=72.5°.
∴直角△ACD中,∠A=90°-22.5°=72.5°,
同理,∠B=22.5°.
∵直角△ABC中,CE为AB边上的中线,
∴CE=
AB=BE,
∴∠BCE=∠B=22.5°,
∴∠DCE=∠DCB-∠BCE=45°,
又∵∠CED=∠B+∠BCE=22.5°+22.5°=45°,
∴∠DCE=∠CED,
∴DE=DC.
 解:∵∠ACB=90°且∠BCD=3∠DCA,
解:∵∠ACB=90°且∠BCD=3∠DCA,∴∠ACD=90°×
| 1 |
| 4 |
∴直角△ACD中,∠A=90°-22.5°=72.5°,
同理,∠B=22.5°.
∵直角△ABC中,CE为AB边上的中线,
∴CE=
| 1 |
| 2 |
∴∠BCE=∠B=22.5°,
∴∠DCE=∠DCB-∠BCE=45°,
又∵∠CED=∠B+∠BCE=22.5°+22.5°=45°,
∴∠DCE=∠CED,
∴DE=DC.
点评:本题考查了直角三角形的性质,直角三角形的斜边上的中线等于斜边的一半,以及等腰三角形的判定,正确求得∠DCE的度数是关键.

练习册系列答案
相关题目
下列方程中是一元二次方程的有( )
①4x2=x ②2x2xy+4=0 ③x2=0 ④
-
=2 ⑤6x(x-5)=6x2.
①4x2=x ②2x2xy+4=0 ③x2=0 ④
| 1 |
| x2 |
| 1 |
| x |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图:将等腰梯形ABCD的一条对角线BD平移CE的位置,△CAE是等腰三角形吗?为什么?
如图:将等腰梯形ABCD的一条对角线BD平移CE的位置,△CAE是等腰三角形吗?为什么?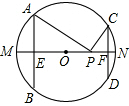 如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN 于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值为
如图,AB、CD是半径为10的圆O的两条弦,AB=16,CD=12,MN是直径,AB⊥MN 于点E,CD⊥MN于F,P为EF上任意一点,求PA+PC的最小值为 如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为
如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为 小红和小兰房间窗户的装饰物(装饰物不能透光)如图1和2,它们分别由两个四分之一的圆和四个半圆组成(半径相同).
小红和小兰房间窗户的装饰物(装饰物不能透光)如图1和2,它们分别由两个四分之一的圆和四个半圆组成(半径相同).