题目内容
 如图,四边形ABCD中,AB=3cm,BC=4cm,DA=13cm,CD=12cm,且∠ABC=90°,则四边形ABCD的面积为( )
如图,四边形ABCD中,AB=3cm,BC=4cm,DA=13cm,CD=12cm,且∠ABC=90°,则四边形ABCD的面积为( )| A、84 | ||
| B、36 | ||
C、
| ||
| D、无法确定 |
考点:勾股定理,勾股定理的逆定理
专题:计算题
分析:连接AC,在直角三角形ABC中,由AB与BC的长,利用勾股定理求出AC的长,在三角形ACD中,利用勾股定理的逆定理判断出三角形ACD为直角三角形,两直角三角形面积之和即为四边形ABCD面积,求出即可.
解答: 解:连接AC,
解:连接AC,
在Rt△ABC中,AB=3cm,BC=4cm,
根据勾股定理得:AC=
=5cm,
∵DA=13cm,CD=12cm,
∴DA2=CD2+AC2,
∴△ACD为直角三角形,
则S四边形ABCD=S△ABC+S△ACD=
×3×4+
×12×5=36cm2,
故选B
 解:连接AC,
解:连接AC,在Rt△ABC中,AB=3cm,BC=4cm,
根据勾股定理得:AC=
| 32+42 |
∵DA=13cm,CD=12cm,
∴DA2=CD2+AC2,
∴△ACD为直角三角形,
则S四边形ABCD=S△ABC+S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
故选B
点评:此题考查了勾股定理,以及勾股定理逆定理,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1<x2,有下列结论:
①x1=2,x2=3;②m>-
;③当m>0时,x1<2<3<x2;④二次函数y=(x-x1)(x-x2)+m图象与x轴交点的坐标为(2,0)和(3,0).
其中一定成立的结论是( )
①x1=2,x2=3;②m>-
| 1 |
| 4 |
其中一定成立的结论是( )
| A、①③④ | B、②③④ |
| C、②③ | D、②④ |
下列说法错误的是( )
| A、过直线外一点有且仅有一条直线与它平行 |
| B、在同一平面内,不同的两条直线只有一个交点 |
| C、经过一点有且只有一条直线与已知直线垂直 |
| D、经过两点有且只有一条直线 |
 四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )
四边形ABCD中,下列条件不能判定四边形ABCD是平行四边形的是( )| A、AB∥CD,AD∥BC |
| B、AB∥CD,AB=CD |
| C、AB=CD,AD=BC |
| D、AD∥BC,AB=CD |
下列计算正确的是( )
| A、(a3)3=a6 |
| B、a3•a3=a9 |
| C、a3+a3=2a6 |
| D、a2•(a3)2=a8 |
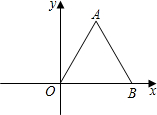 如图,将边长为4的等边三角形OAB先向下平移3个单位,再将平移后的图形沿y轴翻折,经过两次变换后,点A的对应点A′的坐标为( )
如图,将边长为4的等边三角形OAB先向下平移3个单位,再将平移后的图形沿y轴翻折,经过两次变换后,点A的对应点A′的坐标为( )A、(2,3-2
| ||
| B、(2,1) | ||
C、(-2,2
| ||
D、(-1,2
|
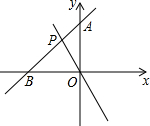 如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(-1,-m),则关于x的不等式组mx>kx+b>mx-2的解集为( )
如图,直线y1=kx+b过点A(0,2)且与直线y2=mx交于点P(-1,-m),则关于x的不等式组mx>kx+b>mx-2的解集为( )| A、x<-1 |
| B、-2<x<0 |
| C、-2<x<-1 |
| D、x<-2 |
如图,把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形,仅剩下的三个小三角形再重复以上做法…一直到第六次挖去后剩下的三角形有( )个.


| A、35 |
| B、35+1 |
| C、36 |
| D、36+1 |