题目内容
16.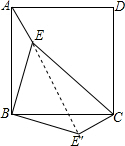 如图,点E是正方形ABCD内的一点,点E′在BC边的下方,连接AE,BE,CE,BE′,CE′.若AE=1,BE=2,CE=3,且△ABE≌△CBE′,则∠BE′C=135°.
如图,点E是正方形ABCD内的一点,点E′在BC边的下方,连接AE,BE,CE,BE′,CE′.若AE=1,BE=2,CE=3,且△ABE≌△CBE′,则∠BE′C=135°.
分析 先由勾股定理的逆定理证得△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
解答 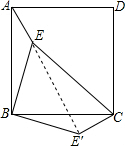 解:连接EE′
解:连接EE′
∵△ABE≌△CBE′,
∴∠ABE=∠CBE′,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠EBE′=90°,
∴△EBE′是直角三角形,
又∵△ABE≌△CBE′,
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
∵EE′2=22+22=8,AE=CE′=1,EC=3,
∴EC2=E′C2+EE′2,
∴△EE′C是直角三角形,
∴∠EE′C=90°,
∴∠AEB=135°,
故答案为:135.
点评 本题考查了正方形的性质、全等三角形的性质、勾股定理的逆定理;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
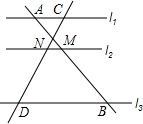 如图,l1∥l2∥l3,AM=2,MB=3,CN=1.8,则CD=4.5.
如图,l1∥l2∥l3,AM=2,MB=3,CN=1.8,则CD=4.5. 如图,将n张长为a cm的纸片一张一张地贴成一个长纸条,每两张纸片重合部分的长度为bcm,试估计贴成的纸条的长度并计算.
如图,将n张长为a cm的纸片一张一张地贴成一个长纸条,每两张纸片重合部分的长度为bcm,试估计贴成的纸条的长度并计算.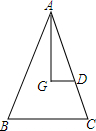 如图,G是△ABC重心,GD∥BC交AC于D,则S△ADG:S△ABC=$\frac{2}{9}$.
如图,G是△ABC重心,GD∥BC交AC于D,则S△ADG:S△ABC=$\frac{2}{9}$.