题目内容
8.已知直角三角形的两边长分别为6和8,则这个直角三角形的周长是( )| A. | 24或14+2$\sqrt{7}$ | B. | 24 | C. | 20或14-2$\sqrt{7}$ | D. | 22或14+2$\sqrt{7}$ |
分析 先根据勾股定理求得斜边的长,注意题中没有指明已知的两边是直角边还是斜边故应该分情况进行讨论.
解答 解:①当6和8均为直角边时,斜边=$\sqrt{{6}^{2}+{8}^{2}}$=10,
则这个直角三角形的周长是:6+8+10=24;
②当6为直角边,8为斜边时,
则斜边为:$\sqrt{{8}^{2}-{6}^{2}}$=2$\sqrt{7}$.
故这个直角三角形的周长是:14+2$\sqrt{7}$.
故选:A.
点评 此题主要考查了勾股定理,正确分类讨论求出直角三角形的周长是解题关键.

练习册系列答案
相关题目
3.若一次函数y=(m-1)x+m2-1的图象通过原点,则m的值为( )
| A. | m=-1 | B. | m=1 | C. | m=±1 | D. | m≠1 |
18.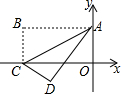 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
 如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )
如图,已知矩形纸片OABC在平面直角坐标系中,将该纸片沿对角线AC进行折叠,使得点B到达点D的位置,若该纸片的长为4、宽为2,则点D的坐标为( )| A. | (-$\frac{12}{5}$,-$\frac{6}{5}$) | B. | (-$\frac{12}{5}$,-$\frac{8}{5}$) | C. | ($\frac{12}{5}$,-$\frac{6}{5}$) | D. | ($\frac{12}{5}$,-$\frac{8}{5}$) |

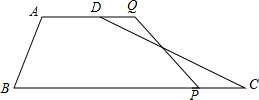 如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.
如图,在四边形ABCD中,AD∥BC AD=5cm,BC=8cm,M是CD的中点,P是BC边上一个动点(P与B,C不重合)连接PM并延长交AD的延长线于Q.