题目内容
13.某同学练习折返跑,从选定的初始位置出发,向前记作正数,返回记作负数,他折返的记录如下(单位:m):+5、-3、+10、-8、-6、+12、-10.求:(1)该同学是否回到初始的位置?
(2)该同学离开初始位置最远是多少?
(3)该同学共跑了多少米?
分析 (1)由于某同学从选定的初始位置出发练习折返跑,问最后是否回到了选定的初始位置,只需将所有数加起来,看其和是否为0即可;
(2)计算每一次跑后的数据,绝对值最大的即为所求;
(3)求出所有数的绝对值的和即可.
解答 解:根据题意得
(1)5-3+10-8-6+1-10=0,
故回到了初始位置;
(2)离开初始位置最远是12米;
(3)总路程=|5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=54米.
点评 此题考查了正数和负数,在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.“正”和“负”相对.解题关键是理解“正”和“负”的相对性,确定具有相反意义的量.

练习册系列答案
相关题目
1.若直线y=kx+b经过A(0,2)和B(3,0)两点,那么这个一次函数关系式是( )
| A. | y=2x+3 | B. | y=3x+2 | C. | y=-$\frac{2}{3}$x+2 | D. | y=x-1 |
8.连续掷两枚硬币,结果都是正面朝上的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
18.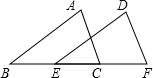 如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
 如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )
如图,BE=CF,AB=DE,添加下列哪个条件可以使△ABC≌△DEF( )| A. | AC=DF | B. | ∠A=∠D | C. | AC∥DF | D. | BC=EF |
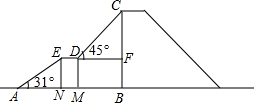 如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
如图,是某儿童乐园为小朋友设计的滑梯平面图.已知BC=5米,AB=8米,中间平台宽度DE=1米,EN、DM、CB为三根垂直于AB的支柱,垂足分别为N、M、B,∠EAB=31°,DF⊥BC于F,∠CDF=45°.求DM和BC的水平距离BM的长度.(结果精确到0.1米,参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)