题目内容
15. 抛物线L:y=a(x-x1)(x-x2)(常数a≠0)与x轴交于点A(x1,0),B(x2,0),与y轴交于点C,且x1•x2<0,AB=4,当直线l:y=-3x+t+2(常数t>0)同时经过点A,C时,t=1.
抛物线L:y=a(x-x1)(x-x2)(常数a≠0)与x轴交于点A(x1,0),B(x2,0),与y轴交于点C,且x1•x2<0,AB=4,当直线l:y=-3x+t+2(常数t>0)同时经过点A,C时,t=1.(1)点C的坐标是(0,3);
(2)求点A,B的坐标及L的顶点坐标;
(3)在如图2 所示的平面直角坐标系中,画出L的大致图象;
(4)将L向右平移t个单位长度,平移后y随x的增大而增大部分的图象记为G,若直线l与G有公共点,直接写出t的取值范围.
分析 (1)把t=1代入y=-3x+t+2,令x=0,求得相应的y值,即可得到点C的坐标;
(2)根据待定系数法,可得函数解析式;
(3)根据描点法,可得函数图象;
(3)根据平移规律,可得G的解析式,根据函数与不等式的关系,可得答案.
解答 解:(1)直线的解析式为y=-3x+3,
当x=0时,y=3,即C点坐标为(0,3),
故答案为:(0,3),
(2)当y=0时,-3x+3=0,解得x1=1,即A(1,0),
由点A(x1,0),B(x2,0),且x1•x2<0,AB=4,
得1-x2=4,解得x2=-3,即B(-3,0);
L:y=a(x-1)(x+3),将C(0,3)坐标代入L,得a=-1,
∴L的解析式为y=-(x-1)(x+3),
即y=-(x+1)2+4
∴L的顶点坐标为(-1,4);
(3)函数图象如图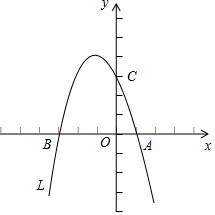 ;
;
(4)L向右平移t个单位的解析式为y=-(x+1-t)2+4,
a=-1<0,当x≥t-1时,y随x的增大而增大.
若直线l与G有公共点时,则有当x=-1+t时,G在直线l的上方,
即-(t-1+1-t)2+4≥-3(t-1)+t+2,
解得t≥$\frac{1}{2}$.
点评 本题考查了二次函数综合题,解(1)的关键是利用自变量与函数值的对应关系;解(2)的关键是待定系数法;解(3)的关键是描点法,解(4)的关键是利用函数值的大小得出不等式,还利用了函数图象平移的规律.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
4.某班抽取6名学生参加体能测试,成绩如下:80,90,75,75,80,80,下列表述错误的是( )
| A. | 平均数是80 | B. | 极差是15 | C. | 中位数是80 | D. | 众数是75 |
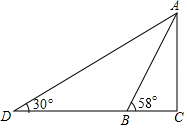 如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
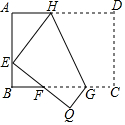 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.
如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AB=6,AE=4,则△EBF周长的大小为8.