题目内容
4.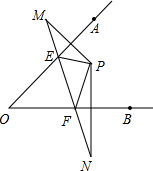 如图,点P在∠AOB的内部,作点P关于直线OA、OB的对称点M,N,连结MN交OA、OB于点E、F.
如图,点P在∠AOB的内部,作点P关于直线OA、OB的对称点M,N,连结MN交OA、OB于点E、F.(1)如果△PEF的周长是20cm,求线段MN的长;
(2)如果∠AOB=45°,连结OM、OP、ON,你能求出∠MON的角度吗?
分析 (1)根据轴对称的性质可知:EP=EM,PF=FN,所以线段MN的长=△PEF的周长;
(2)结合线段垂直平分线的性质和等腰三角形的性质推知OP=OM,∠MOA=∠AOP,同理,∠BOP=∠BON,则∠MON=2∠AOB=90°.
解答 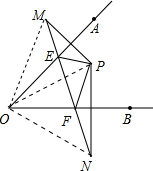 解:(1)根据题意,EP=EM,PF=FN,
解:(1)根据题意,EP=EM,PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm;
(2)如图,连接OP、OM、ON.
∵OA垂直平分MP,
∴OP=OM,
∴∠MOA=∠AOP,
同理,∠BOP=∠BON,
∵∠AOB=∠AOP+∠BOP=45°.
∴∠MON=2∠AOB=90°.
点评 本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
12.下列条件能让两个三角形全等的是( )
| A. | 有一边和两角对应相等 | B. | 有两边和一角对应相等 | ||
| C. | 三个角对应相等 | D. | 面积相等且有一边相等 |
14.点M(3,8)关于x轴对称的点的坐标为( )
| A. | (-3,-8) | B. | (-3,8) | C. | (3,-8) | D. | (3,8) |
 如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.
如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.