题目内容
完成下面的证明.
(1)如图①,点D,E,F分别是三角形ABC的,CA,AC点B上的边B.DE∥BA,DF∥CA,求证∠FDE=∠A.
证明:∵DE∥BA,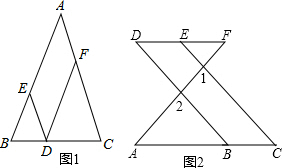
∴∠FDE=
∵DF∥CA,
∴∠A=
∴∠FDE=∠A.
(2)如图②,AC,AF,DF,BC,CE都是直线,∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2,
∴BD∥CE
∴∠C=∠ABD
∵∠C=∠D,
∴∠D=
∴DF∥AC
∴∠A=∠F
(1)如图①,点D,E,F分别是三角形ABC的,CA,AC点B上的边B.DE∥BA,DF∥CA,求证∠FDE=∠A.
证明:∵DE∥BA,

∴∠FDE=
∠CFD
∠CFD
∵DF∥CA,
∴∠A=
∠CFD
∠CFD
∴∠FDE=∠A.
(2)如图②,AC,AF,DF,BC,CE都是直线,∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2,
∴BD∥CE
(同位角相等,两直线平行)
(同位角相等,两直线平行)
.∴∠C=∠ABD
(两直线平行,同位角相等)
(两直线平行,同位角相等)
.∵∠C=∠D,
∴∠D=
∠ABD
∠ABD
(等量代换).∴DF∥AC
(内错角相等,两直线平行)
(内错角相等,两直线平行)
.∴∠A=∠F
(两直线平行,内错角相等)
(两直线平行,内错角相等)
.分析:(1)根据平行线的性质得出∠FDE=∠CFD,∠A=∠CFD,即可推出答案;
(2)根据平行线的判定推出BD∥CE,根据平行线性质得出∠C=∠ABD=∠D,根据平行线的判定推出∠DF∥AC,根据平行线的性质推出即可.
(2)根据平行线的判定推出BD∥CE,根据平行线性质得出∠C=∠ABD=∠D,根据平行线的判定推出∠DF∥AC,根据平行线的性质推出即可.
解答:(1)证明:∵DE∥AC,
∴∠FDE=∠CFD,
∵DF∥AB,
∴∠A=∠CFD,
∴∠FDE=∠A,
(2)证明:∵∠1=∠2,
∴BD∥CE(同位角相等,两直线平行),
∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D,
∴∠D=∠ABD,
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案为::∠CFD,∠CFD;(同位角相等,两直线平行),(两直线平行,同位角相等),∠ABD,(内错角相等,两直线平行),(两直线平行,内错角相等).
∴∠FDE=∠CFD,
∵DF∥AB,
∴∠A=∠CFD,
∴∠FDE=∠A,
(2)证明:∵∠1=∠2,
∴BD∥CE(同位角相等,两直线平行),
∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D,
∴∠D=∠ABD,
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等),
故答案为::∠CFD,∠CFD;(同位角相等,两直线平行),(两直线平行,同位角相等),∠ABD,(内错角相等,两直线平行),(两直线平行,内错角相等).
点评:本题考查了对平行线的性质和判定的应用,注意:平行线的性质定理有①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 25、如图:
25、如图: 完成下面的证明过程
完成下面的证明过程 
 如图,∠1=∠2,∠3=∠4,∠A=100°,求x的值.
如图,∠1=∠2,∠3=∠4,∠A=100°,求x的值. 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G. 完成下面的证明.
完成下面的证明.