题目内容
18.先化简,再求代数式($\frac{1}{x+y}$-$\frac{3}{xy+{y}^{2}}$)÷$\frac{9-3y}{y}$的值,其中x=2sin60°-1,y=tan45°.分析 先将分子、分母因式分解、将括号内通分,同时将除法转化为乘法,再计算括号内的减法,最后约分可得,将x、y的值整理后代入即可.
解答 解:原式=[$\frac{y}{y(x+y)}$-$\frac{3}{y(x+y)}$]•$\frac{y}{-3(y-3)}$
=$\frac{y-3}{y(x+y)}$•$\frac{y}{-3(y-3)}$
=-$\frac{1}{3(x+y)}$
=-$\frac{1}{3x+3y}$,
∵x=2sin60°-1=2×$\frac{\sqrt{3}}{2}$-1=$\sqrt{3}$-1,y=tan45°=1,
∴原式=-$\frac{1}{3(\sqrt{3}-1)+3}$=-$\frac{1}{3\sqrt{3}}$=-$\frac{\sqrt{3}}{9}$.
点评 本题主要考查分式的化简求值,熟练掌握分式的混合运算的顺序和运算法则是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
9.下列结论中正确的是( )
| A. | 数轴上任何一个点都表示唯一的有理数 | |
| B. | 两个无理数的乘积一定是无理数 | |
| C. | 两个无理数之和一定是无理数 | |
| D. | 数轴上的点和实数是一一对应的 |
6.下列说法中,正确的是( )
| A. | 两边及其中一边的对角分别相等的两个三角形全等 | |
| B. | 两边及其中一边上的高分别相等的两个三角形全等 | |
| C. | 斜边和一锐角分别相等的两个直角三角形全等 | |
| D. | 面积相等的两个三角形全等 |
3.在下列各数中:0,3.1415926,$\frac{22}{7}$,π,15%,-2.363636…,正分数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
10.成年人一年心跳的正常次数约为36792000次,用科学记数法表示为( )
| A. | 3.6792×108 | B. | 3679.2×104 | C. | 3.6792×107 | D. | 0.36792×108 |
8.下列说法不正确的是( )
| A. | 任何有理数都有绝对值 | B. | 整数、分数统称有理数 | ||
| C. | 最大的负数是-1 | D. | 零是最小的自然数 |
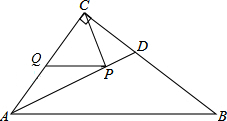 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=8,AD是∠BAC的平分线,若点P,Q分别是AD和AC上的动点,则PC+PQ的最小值是4.