题目内容
20.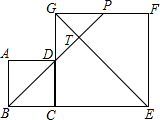 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )
如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交BG于点T,交FG于点P,则ET的值为( )| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 6$\sqrt{2}$ |
分析 根据正方形的对角线平分一组对角可得∠ADB=∠CGE=45°,再求出∠GDT=45°,从而得到△DGT是等腰直角三角形,根据正方形的性质求出DG、GE,再根据等腰直角三角形的直角边等于斜边的$\frac{\sqrt{2}}{2}$倍求出GT,即可得出ET的值.
解答 解:∵BD、GE分别是正方形ABCD,正方形CEFG的对角线,
∴∠ADB=∠CGE=45°,
∴∠GDT=180°-90°-45°=45°,
∴∠DTG=180°-∠GDT-∠CGE=180°-45°-45°=90°,
∴△DGT是等腰直角三角形,
∵两正方形的边长分别为4,8,
∴DG=8-4=4,GE=8$\sqrt{2}$,
∴GT=$\frac{\sqrt{2}}{2}$×4=2$\sqrt{2}$.
∴ET=GE-GT=8$\sqrt{2}$-2$\sqrt{2}$=6$\sqrt{2}$.
故选:D.
点评 本题考查了正方形的性质,等腰直角三角形的判定与性质.熟练掌握正方形的性质,证明等腰直角三角形是解决问题的关键.

练习册系列答案
相关题目
11.二次函数y=$\frac{1}{2}(x-3)^{2}$的图象的开口方向,对称轴分别是( )
| A. | 向上,直线x=3 | B. | 向下,直线x=3 | C. | 向上,直线x=-3 | D. | 向下,直线x=-3 |
5.函数y=mx+n与y=nx的大致图象是( )
| A. | 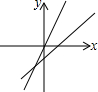 | B. | 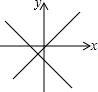 | C. | 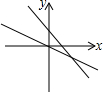 | D. |  |
9.我国嫦娥三号探测器发射总质量约为3700千克,3700用科学记数法表示为( )
| A. | 3.7×102 | B. | 3.7×103 | C. | 37×102 | D. | 0.37×104 |

 已知如图,图中共有9个角,它们分别是∠A、∠1、∠ABE、∠2、∠DBC、∠3、∠C、∠D、∠E.
已知如图,图中共有9个角,它们分别是∠A、∠1、∠ABE、∠2、∠DBC、∠3、∠C、∠D、∠E.