题目内容
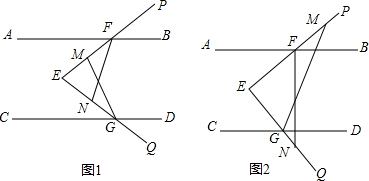
10.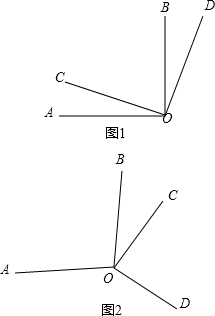 如图(1),已知OA⊥OB,OC⊥OD,试说明∠AOD+∠BOC=180°.
如图(1),已知OA⊥OB,OC⊥OD,试说明∠AOD+∠BOC=180°.证明:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°(垂直的定义)
∴∠AOD+∠BOC=(∠AOB+∠BOD)+(∠COD-∠BOD)=∠AOB+∠COD=180°.
如图(2)已知OA⊥OB,OC⊥OD,试猜想∠AOD+∠BOC=180°.
说明理由.
分析 利用垂线的定义以及圆周角的定义分别分析求出即可.
解答 解:如图(1),
证明:∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°( 垂直的定义)
∴∠AOD+∠BOC=(∠AOB+∠BOD)+(∠COD-∠BOD)=∠AOB+∠COD=180°.
如图(2)已知OA⊥OB,OC⊥OD,则∠AOD+∠BOC=180°.
理由:∵∵OA⊥OB,OC⊥OD,
∴∠AOB=∠COD=90°,
∵∠AOD+∠BOC+∠AOB+COD=360°,
∴∠AOD+∠BOC+180°=360°,
∴∠AOD+∠BOC=180°.
故答案为:垂直的定义,BOD,180,180.
点评 此题主要考查了垂直的定义以及圆周角定理,利用数形结合得出是解题关键.

练习册系列答案
相关题目
20.黄冈市地处湖北省东部,大别山南麓,长江北岸,下辖一区七县两市,总人口740万人,人口总数用科学记数法表示为( )
| A. | 70.4×105人 | B. | 7.4×106人 | C. | 7.4×105人 | D. | 7.4×104人 |
1.有一个底面半径为3cm,母线长10cm的圆锥,则其侧面积是( )
| A. | 30cm2 | B. | 30πcm2 | C. | 15πcm2 | D. | 15cm2 |
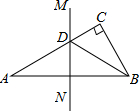 如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( )
如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( ) 如图,在正方形ABCD中,AB=a,M为AB的中点,ED=3AE.
如图,在正方形ABCD中,AB=a,M为AB的中点,ED=3AE.