题目内容
5.已知△ABC中,点D在边BC上,且BD=2DC.设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,那么$\overline{AD}$等于$\overrightarrow a+\frac{2}{3}\overrightarrow b$(结果用$\overrightarrow a$、$\overrightarrow b$表示).分析 首先根据题意画出图形,由BD=2DC,可求得$\overrightarrow{BD}$,再利用三角形法则求解即可求得答案.
解答  解:如图,∵$\overrightarrow{BC}=\overrightarrow b$,BD=2DC,
解:如图,∵$\overrightarrow{BC}=\overrightarrow b$,BD=2DC,
∴$\overrightarrow{BD}$=$\frac{2}{3}$$\overrightarrow{BC}$=$\frac{2}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$.
故答案为:$\overrightarrow{a}$+$\frac{2}{3}$$\overrightarrow{b}$.
点评 此题考查了平面向量的知识.注意掌握三角形法则的应用是解此题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
15.二次函数y=$\frac{1}{2}$x2-2的最小值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
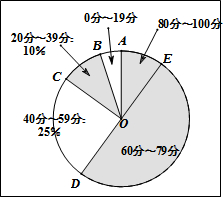 如图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
如图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.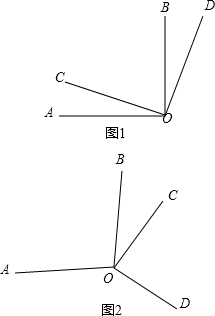 如图(1),已知OA⊥OB,OC⊥OD,试说明∠AOD+∠BOC=180°.
如图(1),已知OA⊥OB,OC⊥OD,试说明∠AOD+∠BOC=180°.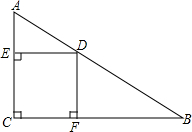 已知Rt△ABC中,∠ACB=90°,CD平分∠ACB,且DE⊥AC,DF⊥BC,求证:四边形DECF是正方形.
已知Rt△ABC中,∠ACB=90°,CD平分∠ACB,且DE⊥AC,DF⊥BC,求证:四边形DECF是正方形.