题目内容
12.某商店销售一种商品,每件的进价为2.00元,根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是10.00元时,销售量为500件,而单价每降低1元,就可多销售出200件.请你分析,销售单价多少时,可以获利最大.分析 根据等量关系“利润=(售价-进价)×(500+200×降价)”列出函数关系式.根据函数关系式求得利润最大值.
解答 解:根据题意得:y=(x-2)[(500+200(10-x)]
=-200x2+2900x-5000
=-200(x-$\frac{29}{4}$)2+5512.5,
∵a=-200<0,
∴当x=7.25时,y取最大值,最大值是5512.5,
即售价7.25时利润最大,
∴销售单价为7.25元时,最大利润5512.5元.
点评 本题考查了二次函数的应用,运用数学建模思想把实际问题转化为数学问题.运用函数性质求最值常用公式法或配方法.

练习册系列答案
相关题目
20.下列多项式中能用提公因式法分解的是( )
| A. | x2+y2 | B. | x2-y2 | C. | x2+2x+1 | D. | x2+2x |
17. 如图,D是⊙O的直径,A、B是⊙O上的两点,若∠ADC=80°,则∠ABD的度数为( )
如图,D是⊙O的直径,A、B是⊙O上的两点,若∠ADC=80°,则∠ABD的度数为( )
 如图,D是⊙O的直径,A、B是⊙O上的两点,若∠ADC=80°,则∠ABD的度数为( )
如图,D是⊙O的直径,A、B是⊙O上的两点,若∠ADC=80°,则∠ABD的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
4.若二次函数y=ax2+ax-1的最小值为-$\frac{7}{4}$,则a的值是( )
| A. | -1 | B. | 0 | C. | 3 | D. | 3或-1 |
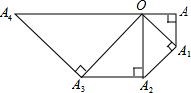 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.