题目内容
3.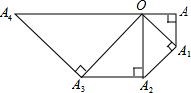 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.
分析 利用等腰直角三角形的性质以及勾股定理分别求出各边长,进而得出答案.
解答 解:∵△OAA1为等腰直角三角形,OA=1,
∴AA1=OA=1,OA1=$\sqrt{2}$OA=$\sqrt{2}$;
∵△OA1A2为等腰直角三角形,
∴A1A2=OA1=$\sqrt{2}$,OA2=$\sqrt{2}$OA1=2;
∵△OA2A3为等腰直角三角形,
∴A2A3=OA2=2,OA3=$\sqrt{2}$OA2=2$\sqrt{2}$;
∵△OA3A4为等腰直角三角形,
∴A3A4=OA3=2$\sqrt{2}$,OA4=$\sqrt{2}$OA3=4.
∵△OA4A5为等腰直角三角形,
∴A4A5=OA4=4,OA5=$\sqrt{2}$OA4=4$\sqrt{2}$.
∵△OA5A6为等腰直角三角形,
∴A5A6=OA5=4$\sqrt{2}$,OA6=$\sqrt{2}$OA5=8.
∴OA10的长度为$\sqrt{{2}^{10}}=32$.
故答案为:32.
点评 此题主要考查了等腰直角三角形的性质以及勾股定理,熟练应用勾股定理得出是解题关键.

练习册系列答案
相关题目
11.下列图形中不是轴对称图形的是( )
| A. | 等边三角形 | B. | 正方形 | C. | 平行四边形 | D. | 正五边形 |
18.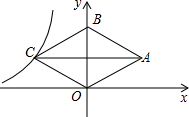 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | -12 | B. | -6 | C. | 6 | D. | 12 |
8.关于x的方程4x-2m+1=5x-8的解集是负数,则m的取值范围是( )
| A. | m>$\frac{9}{2}$ | B. | m<0 | C. | m$<\frac{9}{2}$ | D. | m>0 |
13.当分式$\frac{x+2}{x-1}$的值为0时,x的值是( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
 如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为25°.
如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为25°.