题目内容
7.已知在△ABC中,∠ACB=90°,CA=CB,CD⊥AB于D.(1)按要求补全图1,若点E是线段CD上任意一点(不与端点重合),①过点E作EF⊥CD交AC于F;②连接BF;③取BF中点G,连接EG;
(2)判断(1)中EG与BC的位置关系并证明;
(3)将(1)中的△CEF绕点C旋转到如图2的位置,其它条件不变,判断EG与AF的数量关系并证明.

分析 (1)补全的图如图1所示.
(2)如图1中,结论:EG∥BC.延长FE交BC于H.只要证明FE=EH,即可利用三角形中位线定理证明.
(3)结论:AF=2EG.延长FE到H,使得EH=EF,连接CH、BH.首先证明BH=2EG,再证明△ACF≌△BCH,推出AF=BH即可解决问题.
解答 解:(1)补全的图如图1所示.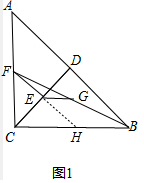
(2)如图1中,结论:EG∥BC.
理由:延长FE交BC于H.
∵CA=CB,∠ACB=90°,CD⊥AB,
∴∠ACD=∠BCD=45°,
∵EF⊥CD,
∴∠CEF=∠CEH=90°,
∴∠CFH=∠CHF=45°,
∴CF=CH,∵CE⊥FH,
∴EF=EH,∵FG=GB,
∴EG∥BH,
∴EG∥BC.
(3)结论:AF=2EG.理由如下:
如图2中,延长FE到H,使得EH=EF,连接CH、BH.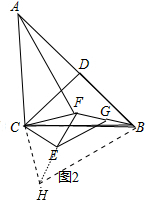
∵EF=EH,FG=GB,
∴BH=2EG,
∵△CEF是等腰直角三角形,
∴CE=EF=EH,CE⊥FH,
∴CF=CH,∠FCH=∠ACB=90°,
∴∠ACF=∠BCH,
在△ACF和△BCH中,
$\left\{\begin{array}{l}{AC=CB}\\{∠ACF=∠BCH}\\{CF=CH}\end{array}\right.$,
∴△ACF≌△BCH,
∴AF=BH,∵BH=2EG,
∴AF=2EG.
点评 本题考查三角形综合题、三角形中位线定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.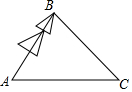 如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
 如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )
如图,为了对一颗倾斜的古杉树AB进行保护,需测量其长度:在地面上选取一点C,测得∠ACB=45°,AC=24m,∠BAC=66.5°,(参考数据:$\sqrt{2}$≈1.414,sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30).则这颗古杉树AB的长约为( )| A. | 7.27 | B. | 16.70 | C. | 17.70 | D. | 18.18 |
12.如a>b,那么下列不等式中正确的是( )
| A. | -$\frac{a}{2}$>-$\frac{b}{2}$ | B. | 2-a<2-b | C. | ac2>bc2 | D. | b-a>0 |
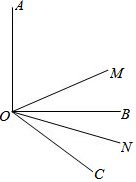 (1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.
(1)如图,已知∠AOB=90°,∠BOC=40°,OM平分∠AOC,ON平分∠BOC.求∠MON的度数.