题目内容
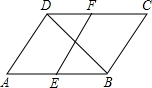 已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点.
已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点.(1)求证:四边形AEFD是平行四边形;
(2)若∠A=60°,AB=8,AD=4,求BD的长.
考点:平行四边形的判定与性质,勾股定理,解直角三角形
专题:
分析:(1)根据平行四边的性质,可得AB与CD的关系,根据线段中点的性质,可得DF与DC,AE与AB的关系,根据平行四边形的判定,可得答案;
(2)根据锐角三角函数,可得AG、DG的长,再根据线段的和差,可得BG的长,根据勾股定理,可得答案.
(2)根据锐角三角函数,可得AG、DG的长,再根据线段的和差,可得BG的长,根据勾股定理,可得答案.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD且AB=CD.
∵点E,F分别是AB,CD的中点,
∴AE=
AB,DF=
CD.
∴AE=DF.
∴四边形AEFD是平行四边形.
(2)解:过点D作DG⊥AB于点G, ,
,
在Rt△AGD中,
∵∠AGD=90°,∠A=60°,
AD=4,
∴AG=ADcos60°=2,
DG=ADsin60°=2
∵AB=8,
∴BG=AB-AG=6.
在Rt△DGB中,
∠DGB=90°,DG=2
,BG=6,
∴DB=
=
=4
.
∴AB∥CD且AB=CD.
∵点E,F分别是AB,CD的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=DF.
∴四边形AEFD是平行四边形.
(2)解:过点D作DG⊥AB于点G,
 ,
,在Rt△AGD中,
∵∠AGD=90°,∠A=60°,
AD=4,
∴AG=ADcos60°=2,
DG=ADsin60°=2
| 3 |
∵AB=8,
∴BG=AB-AG=6.
在Rt△DGB中,
∠DGB=90°,DG=2
| 3 |
∴DB=
| DG2+BG2 |
| 12+36 |
| 3 |
点评:本题考查了平行四边形的判定与性质,利用了平行四边形的判定与性质,勾股定理,题目较简单.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图,AB与⊙O相切于C,OA=OB,若⊙O的直径为4,AB=2,则OA的长为( )
如图,AB与⊙O相切于C,OA=OB,若⊙O的直径为4,AB=2,则OA的长为( )| A、2 | ||
B、
| ||
C、2
| ||
| D、3 |
已知一个正多边形的每个内角都是144°,则该正多边形的边数是( )
| A、7 | B、8 | C、9 | D、10 |
 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).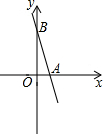 已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.
已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.
 如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°