题目内容
 如图,AB与⊙O相切于C,OA=OB,若⊙O的直径为4,AB=2,则OA的长为( )
如图,AB与⊙O相切于C,OA=OB,若⊙O的直径为4,AB=2,则OA的长为( )| A、2 | ||
B、
| ||
C、2
| ||
| D、3 |
考点:切线的性质
专题:
分析:连接OC,根据切线性质得出OC⊥AB,根据等腰三角形性质求出AC=BC=1,根据勾股定理求出即可.
解答:解:
连接OC,
∵⊙O的直径为4,
∴OC=2,
∵AB与⊙O相切于C,
∴OC⊥AB,
∵OA=OB,AB=2,
∴AC=BC=1,
由勾股定理得:OA=
=
,
故选B.

连接OC,
∵⊙O的直径为4,
∴OC=2,
∵AB与⊙O相切于C,
∴OC⊥AB,
∵OA=OB,AB=2,
∴AC=BC=1,
由勾股定理得:OA=
| 22+12 |
| 5 |
故选B.
点评:本题考查了勾股定理,切线的性质,等腰三角形的性质的应用,注意:圆的切线垂直于过切点的半径.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,几个完全相同的小正方体组成一个几何体,这个几何体的三视图中面积最大的是( )
如图,几个完全相同的小正方体组成一个几何体,这个几何体的三视图中面积最大的是( )| A、主视图 | B、左视图 |
| C、俯视图 | D、主视图和左视图 |
抛物线y=-x2-6x-11的顶点坐标是( )
| A、(3,2) |
| B、(3,-2) |
| C、(-2,2) |
| D、(-3,-2) |
估计7-2
的值在( )
| 6 |
| A、1到2之间 |
| B、2到3之间 |
| C、3到4之间 |
| D、4到5之间 |
 如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,AD=20,则BC的长是( )| A、20 | ||
B、20
| ||
| C、30 | ||
D、10
|
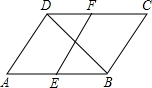 已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点.
已知:如图,在平行四边形ABCD中,点E、F分别是AB、CD的中点. 如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.
如图有A、B两个大小均匀的转盘,其中A转盘被分成3等份,B转盘被分成4等份,并在每一份内标上数字.小明和小红同时各转动其中一个转盘,转盘停止后(当指针指在边界线时视为无效,重转),若将A转盘指针指向的数字记作一次函数表达式中的k,将B转盘指针指向的数字记作一次函数表达式中的b.