题目内容
如图①,△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,CF∥AD.
(1)如图①,∠B=30°,∠ACB=70°,则∠CFE= ;
(2)若(1)中的∠B=α,∠ACB=β,则∠CFE= ;(用α、β表示)
(3)如图②,(2)中的结论还成立么?请说明理由.
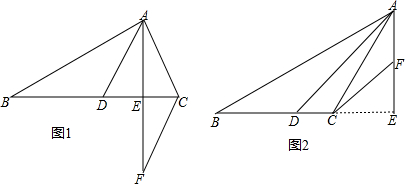
(1)如图①,∠B=30°,∠ACB=70°,则∠CFE=
(2)若(1)中的∠B=α,∠ACB=β,则∠CFE=
(3)如图②,(2)中的结论还成立么?请说明理由.

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)求∠CFE的度数,求出∠DAE的度数即可,只要求出∠BAE-∠BAD的度数,由平分和垂直易得∠BAE和∠BAD的度数即可;
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°-∠ECF解决问题.
(2)由(1)类推得出答案即可;
(3)类比以上思路,把问题转换为∠CFE=90°-∠ECF解决问题.
解答:
解:(1)∵∠B=30°,∠ACB=70°,
∴∠BAC=180°-∠B-∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE-∠BAD=60°-40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°,
(2)∵∠BAE=90°-∠B,∠BAD=
∠BAC=
(180°-∠B-∠BCA)
∴∠CFE=∠DAE=∠BAE-∠BAD=90°-∠B-
(180°-∠B-∠BCA)=
(∠BCA-∠B)=
β-
α.
(3)成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°-α-β,
∵AD平分∠BAC,
∴∠DAC=
∠BAC=90°-
α-
β,
∵CF∥AD,
∴∠ACF=∠DAC=90°-
α-
β,
∴∠BCF=β+90°-
α-
β=90°-
α+
β,
∴∠ECF=180°-∠BCF=90°+
α-
β,
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°-∠ECF=
β-
α.
∴∠BAC=180°-∠B-∠ACB=80°,
∵AD平分∠BAC,
∴∠BAD=40°,
∵AE⊥BC,
∴∠AEB=90°
∴∠BAE=60°
∴∠DAE=∠BAE-∠BAD=60°-40°=20°,
∵CF∥AD,
∴∠CFE=∠DAE=20°,
(2)∵∠BAE=90°-∠B,∠BAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CFE=∠DAE=∠BAE-∠BAD=90°-∠B-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)成立.
∵∠B=α,∠ACB=β,
∴∠BAC=180°-α-β,
∵AD平分∠BAC,
∴∠DAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵CF∥AD,
∴∠ACF=∠DAC=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCF=β+90°-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ECF=180°-∠BCF=90°+
| 1 |
| 2 |
| 1 |
| 2 |
∵AE⊥BC,
∴∠FEC=90°,
∴∠CFE=90°-∠ECF=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查三角形的内角和定理,角平分线的性质,平行线的性质以及垂直的意义等知识,结合图形,灵活选择适当的方法解决问题.

练习册系列答案
相关题目
下列各式:
,
,
,
+m,其中分式共有( )
| x |
| π+2 |
| 5p2 |
| p |
| a2-b2 |
| 2 |
| 1 |
| m |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图所示,∠1=72°,∠2=50°,∠3=72°,求∠4的度数.
如图所示,∠1=72°,∠2=50°,∠3=72°,求∠4的度数.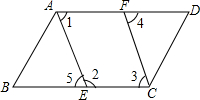 如图,根据图形完成下列填空.
如图,根据图形完成下列填空. 将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是
将单项式a,2a2,3a3,4a4按右侧方式排列,若规定(m,n)表示第m排从左向右第n个单项式,如:(3,2)表示的是a,(5,4)表示的是,则(10,1)与(25,7)的积是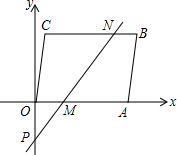 如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.
如图,在平面直角坐标系中,四边形OABC为平行四边形,A(5,0),C(1,4),过点P(0,-2)的直线分别交OA、BC于M、N,且将?OABC的面积分成相等的两部分,求点M,N的坐标.