题目内容
14. 如图,在△ABC中,∠A=70°,点O到AB、BC、AC的距离相等,连接BO、CO,则∠BOC=125°.
如图,在△ABC中,∠A=70°,点O到AB、BC、AC的距离相等,连接BO、CO,则∠BOC=125°.
分析 根据角平分线性质求出O为△ABC三角平分线的交点,根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线定义求出∠OBC+∠OCB,即可求出答案.
解答 解:∵点O到AB、BC、AC的距离相等,
∴OB平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}∠$ABC,∠OCB=$\frac{1}{2}$∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=$\frac{1}{2}×$110°=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
故答案为:125.
点评 本题主要考查平分线的性质,三角形内角和定理的应用,能求出∠OBC+∠OCB的度数是解此题的关键,注意:即角的平分线上的点到角的两边的距离相等.

练习册系列答案
相关题目
5. 如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
 如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )
如图,在△ABC与△DEF中,已知AB=DE,∠A=∠D,还添加一个条件才能使△ABC≌△DEF,下列不能添加的条件是( )| A. | ∠B=∠E | B. | BC=EF | C. | ∠C=∠F | D. | AC=DF |
2.已知代数式4x2-2x+5的值是8,那么代数式6x2-3x-2的值为( )
| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 6 | D. | 5 |
9.以下列各组数为边长,能构成直角三角形的是( )
| A. | 6,8,10 | B. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | C. | 10,15,25 | D. | 7,15,17 |
3.用反证法证明命题“四边形中至少有一个角是钝角或直角”,应先假设( )
| A. | 四边形中没有一个角是钝角或直角 | B. | 四边形中至多有一个钝角或直角 | ||
| C. | 四边形中没有一个角是锐角 | D. | 四边形中没有一个角是钝角 |
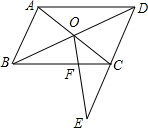 如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( )
如图,在?ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F.已知AB=4,BC=6,CE=2,则CF的长等于( ) 如图是一个正方体的平面展开图,标注了数A的是正方体的正面,如果正方体的左面与右面标注式子相等.
如图是一个正方体的平面展开图,标注了数A的是正方体的正面,如果正方体的左面与右面标注式子相等.