题目内容
探究性问题: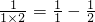 ,
, ,
, ,则
,则 =________.
=________.
试用上面规律,计算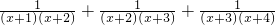 .
.
 -
-
分析:直接根据题意得出规律,再由此规律进行计算即可.
解答:∵
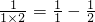 ,
, ,
, ,
,∴
 =
= -
- ;
;∴原式=
 -
-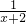 +
+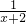 -
-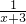 +
+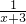 -
-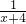
=
 -
-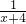
=
 .
.故答案为:
 -
- .
.点评:本题考查的是分式的加减,根据题意找出规律是解答此题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
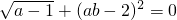 ,求
,求 的值.
的值.