题目内容
 如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为
如图,已知正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,连结BF、CF,则S△BFC的面积为考点:翻折变换(折叠问题),正方形的性质
专题:
分析:根据题意得出S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,进而得出S△BFC=FN,再利用勾股定理得出FN的长,进而得出答案.
解答: 解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,
解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,
∴△ADE≌△AFE,DE=EC=EF=2,AB=AF=4,
过点F作FN⊥CD于点N,FM⊥AB于点M,
∴S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,
∴
×2×4+
×2×4+
×2×FN+
×4×(4-FN)+S△BFC=16,
∴8+FN+8-2FN+S△BFC=16,
∴S△BFC=FN=
×BC×NC=2NC,
设NC=x,则FN=2x,EN=2-x,
∴EF2=EN2+FN2,
∴22=(2-x)2+(2x)2,
解得:x1=0(不合题意舍去),x2=
,
∴FN=2×
=
,
∴S△BFC=
.
故答案为:
.
 解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,
解:∵正方形ABCD的边长为4,点E为边DC的中点,连结AE,将△ADE沿着AE翻折,使点D落在正方形内的点F处,∴△ADE≌△AFE,DE=EC=EF=2,AB=AF=4,
过点F作FN⊥CD于点N,FM⊥AB于点M,
∴S△ADE+S△AFE+S△EFC+S△ABF+S△BFC=4×4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴8+FN+8-2FN+S△BFC=16,
∴S△BFC=FN=
| 1 |
| 2 |
设NC=x,则FN=2x,EN=2-x,
∴EF2=EN2+FN2,
∴22=(2-x)2+(2x)2,
解得:x1=0(不合题意舍去),x2=
| 4 |
| 5 |
∴FN=2×
| 4 |
| 5 |
| 8 |
| 5 |
∴S△BFC=
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:此题主要考查了翻折变换的性质以及三角形面积求法,得出S△BFC=FN是解题关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
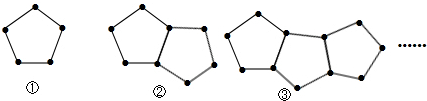
如图,它们是由一些火柴棒搭成的图案,按图①②③所示的规律依次下去,摆第2014个图案用火柴棒的根数是( )

| A、4047 | B、8047 |
| C、4057 | D、8057 |
对于二次函数y=2(x-1)2-3,下列说法正确的是( )
| A、图象开口向下 |
| B、图象和y轴交点的纵坐标为-3 |
| C、x<1时,y随x的增大而减小 |
| D、图象的对称轴是直线x=-1 |

 一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a=
一个有进水管与出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的若干分内既进水又出水,之后只出水不进水.每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图.则a= 如图,在平面直角坐标系中,点A的坐标为(2+
如图,在平面直角坐标系中,点A的坐标为(2+