题目内容
11.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点,若P自点A出发,以1cm/s的速度沿AB方向运动,到B点时停止,同时,Q自点B出发以4cm/s的速度沿BC方向运动,到C点时停止,经过多少秒,以P、B、Q为顶点的三角形占矩形面积的$\frac{1}{4}$?分析 设经过x(0≤x≤3)秒,以P、B、Q为顶点的三角形占矩形面积的$\frac{1}{4}$,则BP=(8-x)cm,PB=4xcm.根据三角形的面积公式结合以P、B、Q为顶点的三角形占矩形面积的$\frac{1}{4}$即可得出关于x的一元二次方程,解之即可得出结论.
解答 解:设经过x(0≤x≤3)秒,以P、B、Q为顶点的三角形占矩形面积的$\frac{1}{4}$, 则BP=(8-x)cm,PB=4xcm.
则BP=(8-x)cm,PB=4xcm.
根据题意得:$\frac{1}{2}$×4x(8-x)=$\frac{1}{4}$×12×8,
整理得:x=2或x=6(舍去).
答:经过2秒,以P、B、Q为顶点的三角形占矩形面积的$\frac{1}{4}$.
点评 本题考查了一元二次方程的应用,根据三角形的面积公式结合△PBQ的面积与矩形面积间的关系列出关于x的一元二次方程是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.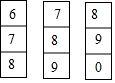 如图是鹏鹏存钱罐的密码锁(每个密码都是0-9中的一个数),该密码锁的一个密码是7,后两位的密码鹏鹏记不清了,他只记得后两位的密码都比6大,则鹏鹏第一次就能打开改密码锁的概率是( )
如图是鹏鹏存钱罐的密码锁(每个密码都是0-9中的一个数),该密码锁的一个密码是7,后两位的密码鹏鹏记不清了,他只记得后两位的密码都比6大,则鹏鹏第一次就能打开改密码锁的概率是( )
 如图是鹏鹏存钱罐的密码锁(每个密码都是0-9中的一个数),该密码锁的一个密码是7,后两位的密码鹏鹏记不清了,他只记得后两位的密码都比6大,则鹏鹏第一次就能打开改密码锁的概率是( )
如图是鹏鹏存钱罐的密码锁(每个密码都是0-9中的一个数),该密码锁的一个密码是7,后两位的密码鹏鹏记不清了,他只记得后两位的密码都比6大,则鹏鹏第一次就能打开改密码锁的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |
16.△ABC三个顶点的坐标分别为A(2,2),B(4,2),C(6,6),在此直角坐标系中作△DEF,使得△DEF与△ABC位似,且以原点O为位似中心,位似比为1:2,则△DEF的面积为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
1.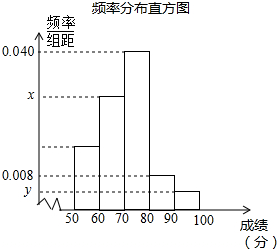 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
 为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图. | 组别 | 分组 | 频数 | 频率 |
| 1 | 50≤x<60 | 9 | 0.18 |
| 2 | 60≤x<70 | a | |
| 3 | 70≤x<80 | 20 | 0.40 |
| 4 | 80≤x<90 | 0.08 | |
| 5 | 90≤x≤100 | 2 | b |
| 合计 |
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
 有理数a,b在数轴上的对应位置如图所示,则下列说法正确的有①④(填序号).
有理数a,b在数轴上的对应位置如图所示,则下列说法正确的有①④(填序号).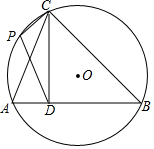 △ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.
△ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.