题目内容
3.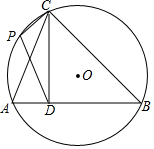 △ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.
△ABC内接于圆O,CD⊥AB于D,CD=DB=3,AD=1,点P为$\widehat{AC}$上一点,求$\frac{\sqrt{10}}{2}$DP+CP的最小值.
分析 如图,作OE⊥CD于E,OF⊥AB于F,连接OP、OA、OC,延长CD交⊙O于M,连接OD延长OD交CA的延长线于K,连接PK.只要证明△POD∽△KOP,可得$\frac{PD}{PK}$=$\frac{OD}{OP}$=$\frac{\sqrt{2}}{\sqrt{5}}$,推出PK=$\frac{\sqrt{10}}{2}$PD,推出PC+$\frac{\sqrt{10}}{2}$=PC+PK,由PC+PK≥KC,可知当点P与点A重合时,PC+PK的值最小,由此即可解决问题.
解答 解:如图,作OE⊥CD于E,OF⊥AB于F,连接OP、OA、OC,延长CD交⊙O于M,连接OD延长OD交CA的延长线于K,连接PK.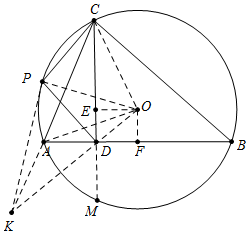
∵CD=DB=3,AD=1,
又∵CD•DM=AD•DB,
∴DM=1,易知四边形OEDF是矩形,
∵CE=EM=2,AF=BF=2,
∴DF=DE=1,
∴四边形OEDF是正方形,
∴OE=1,CO=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∵AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{10}$,
∴AO2+OC2=AC2,
∴∠AOC=90°,
∴∠ODC=∠OCK=45°,∵∠COD=∠COK,
∴△COD∽△KOC,
∴OC2=OD•OK,
∵OP=OC,
∴OP2=OD•OK,∵∠POD=∠POK,
∴△POD∽△KOP,
∴$\frac{PD}{PK}$=$\frac{OD}{OP}$=$\frac{\sqrt{2}}{\sqrt{5}}$,
∴PK=$\frac{\sqrt{10}}{2}$PD,
∴PC+$\frac{\sqrt{10}}{2}$=PC+PK,
∵PC+PK≥KC,
∴当点P与点A重合时,PC+PK的值最小,
∴PC+$\frac{\sqrt{10}}{2}$的最小值=$\frac{\sqrt{10}}{2}$•AD+AC=$\frac{\sqrt{10}}{2}$×1+$\sqrt{10}$=$\frac{3}{2}$$\sqrt{10}$.
点评 本题考查三角形的外接圆与外心、最短问题、相似三角形的判定和性质、垂径定理、正方形的判定和性质等知识,解题的关键是学会添加辅助线,构造相似三角形解决问题,题目比较难,属于竞赛题.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| x/万元 | 30 | 80 | 120 |
| y/万元 | 44 | n | 26 |
(Ⅱ)后来在修建的过程中计划发生改变,决定多修2千米,因此在没有增减建设力量的情况下,修完这条路比计划晚了15天,求原计划每天的修建费.
 如图所示,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3秒时,求△BPQ的面积.
如图所示,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3秒时,求△BPQ的面积.
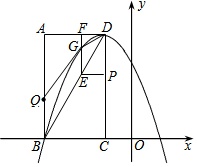 如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.
如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(-3,4)、B(-3,0)、C(-1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.