题目内容
12.图1是棱长为a的小正方体,图2、图3出这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…,第n层,第n层的小正方体的个数为s.(提示:第一层时,s=1;第二层时,s=3)则第n层时,s=$\frac{1}{2}$n(n+1)(用含n的式子表示)
分析 第1个图有1层,共1个小正方体,第2个图有2层,第2层正方体的个数为1+2,根据相应规律可得第3层,第n层正方体的个数.
解答 解:∵第1个图有1层,共1个小正方体,
第2个图有2层,第2层正方体的个数为1+2,
第3个图有3层,第3层正方体的个数为1+2+3,
∴第n层时,s=1+2+3+…+n=$\frac{1}{2}$n(n+1).
故答案为:$\frac{1}{2}$n(n+1).
点评 本题考查图形规律性的变化;得到第n层正方体的个数的规律是解决本题的关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
1.下列数中与-2互为倒数的是( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
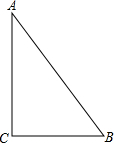 如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.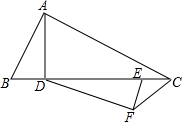 如图,△ABC中,AD为高,∠B=2∠ACB,E为CD上一点,EC=BD,EF∥AB,且E在FC的垂直平分线上,求证:DF⊥EF.
如图,△ABC中,AD为高,∠B=2∠ACB,E为CD上一点,EC=BD,EF∥AB,且E在FC的垂直平分线上,求证:DF⊥EF.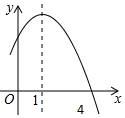 已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.
已知二次函数y=-x2+2x+m的部分图象如图所示,则关于x的一元二次方程-x2+2x+m=0的解为x1=4,x2=-2.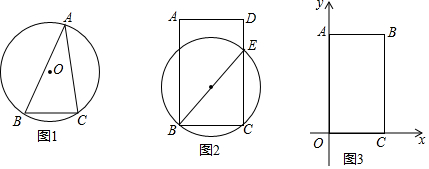
 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是π.
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是π.