题目内容
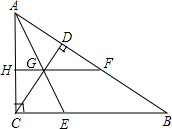 如图,在△ABC中,∠ACB=90°,CD⊥AB于D. 把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D. 把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.(1)判断FH与BC的位置关系,并说明理由;
(2)判断HG与DG的数量关系,并说明理由.
考点:翻折变换(折叠问题)
专题:
分析:(1)连接EF,根据翻折变换的性质可得∠CAE=∠EAF,∠AFE=90°,CE=EF,根据垂直的定义可得∠ADC=90°,然后根据同位角相等,两直线平行判断出EF∥CD,然后根据等角的余角相等求出∠AGD=∠AEC,再求出∠CGE=∠AEC,根据等角对等边可得CG=CE,然后求出CG=EF,再根据一组对边平行且相等的四边形是平行四边形判断出四边形CEFG是平行四边形,根据平行四边形对边平行可得GF∥CE,即FH∥BC;
(2)根据两直线平行,同位角相等可得∠AHG=∠ACB=90°,再根据角平分线上的点到角的两边距离相等可得HG=DG.
(2)根据两直线平行,同位角相等可得∠AHG=∠ACB=90°,再根据角平分线上的点到角的两边距离相等可得HG=DG.
解答: (1)解:如图,连接EF,
(1)解:如图,连接EF,
由翻折的性质得,∠CAE=∠EAF,∠AFE=∠ACB=90°,CE=EF,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠AFE,
∴EF∥CD,
∵∠CAE=∠EAF,∠CAE+∠AEC=∠EAF+∠AGD=90°,
∴∠AGD=∠AEC,
又∵∠AGD=∠CGE(对顶角相等),
∴∠CGE=∠AEC,
∴CE=CG,
∴CG=EF,
∴四边形CEFG是平行四边形,
∴GF∥CE,
即FH∥BC;
(2)解:∵FH∥BC,
∴∠AHG=∠ACB=90°,
又∵∠CAE=∠EAF,
∴HG=DG.
 (1)解:如图,连接EF,
(1)解:如图,连接EF,由翻折的性质得,∠CAE=∠EAF,∠AFE=∠ACB=90°,CE=EF,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠AFE,
∴EF∥CD,
∵∠CAE=∠EAF,∠CAE+∠AEC=∠EAF+∠AGD=90°,
∴∠AGD=∠AEC,
又∵∠AGD=∠CGE(对顶角相等),
∴∠CGE=∠AEC,
∴CE=CG,
∴CG=EF,
∴四边形CEFG是平行四边形,
∴GF∥CE,
即FH∥BC;
(2)解:∵FH∥BC,
∴∠AHG=∠ACB=90°,
又∵∠CAE=∠EAF,
∴HG=DG.
点评:本题考查了翻折变换的性质,主要利用了等角对等边的性质,平行四边形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记各性质并求出四边形CEFG是平行四边形是解题的关键.

练习册系列答案
相关题目
三个数的和大于0,积小于0,那么这三个数中负数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
下列现象中,属于平移现象的为( )
| A、方向盘的转动 |
| B、自行车行驶时车轮的转动 |
| C、钟摆的运动 |
| D、电梯的升降 |
 如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的( )
如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的( )| A、三角形 | B、平行四边形 |
| C、矩形 | D、正方形 |

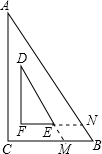 如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.
如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.