题目内容
14. 如图,在△ABC中,AB=AC,∠A=108°,∠B的平分线交AC于点D,求证:DC+AB=BC.
如图,在△ABC中,AB=AC,∠A=108°,∠B的平分线交AC于点D,求证:DC+AB=BC.
分析 在BC上截取,BE=BA,连接DE,首先证明△ABD≌△EBD,从而求得∠DEC=72°,然后再证明△CED为等腰三角形,从而得可证得DC+AB=BC.
解答 解:如图所示,在BC上截取,BE=BA,连接DE.
∵AC平分∠ABC,
∴∠ABD=∠DAE.
在△ABD和△EBD中,$\left\{\begin{array}{l}{AB=BE}\\{∠ABD=∠DAE}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△EBD.
∴∠BED=∠A=108°.
∴∠DEC=180°-108°=72°.
∵AB=AC,
∴∠C=$\frac{1}{2}×(180°-∠A)$=36°,
由三角形的内角和定理可知:∠EDC=180°-36°-72°=72°.
∴∠EDC=∠DEC=72°.
∴DC=EC.
∴DC+AB=BC.
点评 本题主要考查的是全等三角形的性质和判定、等腰三角形的性质和判定,掌握此类问题辅助线的作法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列各数中,是有理数的是( )
| A. | $\root{3}{2}$ | B. | $-\sqrt{3}$ | C. | π | D. | $\frac{1}{3}$ |
19.下列各组数中,不是x+y=5的解的是( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=5}\end{array}\right.$ |
6.下列各式中与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{4}$ |
3.下列实数是无理数的是( )
| A. | -1 | B. | 0 | C. | 3.14 | D. | $\sqrt{5}$ |
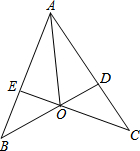 如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.
如图,BD⊥AC,CE⊥AB,垂足分别为D、E,BD与CE相交于点O,AO平分∠BAC.求证:OB=OC.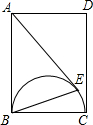 如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.
如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.