题目内容
2.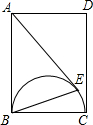 如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.
如图,在矩形ABCD中,AB=3,BC=2,以BC为直径在矩形内作半圆,自点A作半圆的切线AE,则$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.
分析 取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F,则易证AO⊥BE,△BOF∽△AOB,则sin∠CBE=$\frac{CE}{BC}$=$\frac{OF}{OB}$=$\frac{\sqrt{10}}{10}$.
解答 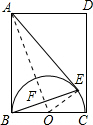 解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F;如图所示:
解:取BC的中点O,则O为圆心,连接OE,AO,AO与BE的交点是F;如图所示:
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴AB是⊙O的切线,
∵AE是⊙O的切线,
∴AE=AB,
在△ABO和△AEO中,
$\left\{\begin{array}{l}{AB=AE}&{\;}\\{OB=OE}&{\;}\\{OA=OA}&{\;}\end{array}\right.$,
∴△ABO≌△AEO(SSS),
∴∠OAB=∠OAE,
∴AO⊥BE,
在Rt△AOB中,OB=$\frac{1}{2}$BC=1,
根据勾股定理得:OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵∠ABO=∠BFO=90°,∠AOB=∠BOF,
∴△BOF∽△AOB,
∴BO:OA=OF:OB,
即1:$\sqrt{10}$=OF:1,
∴OF=$\frac{\sqrt{10}}{10}$,
∵BC是⊙O的直径,
∴∠BEC=90°,
∴sin∠CBE=$\frac{CE}{BC}$=$\frac{OF}{OB}$=$\frac{\sqrt{10}}{10}$,
即$\frac{CE}{BC}$=$\frac{\sqrt{10}}{10}$.
故答案为:$\frac{\sqrt{10}}{10}$.
点评 本题主要考查了切线长定理、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理、三角函数;本题综合性强,有一定难度.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案 如图,已知直线a、b被直线c所截,a∥b,∠2=70°,则∠1=( )
如图,已知直线a、b被直线c所截,a∥b,∠2=70°,则∠1=( )| A. | 110° | B. | 50° | C. | 40° | D. | 60° |
| A. | 6.49×108 | B. | 64.9×107 | C. | 0.649×109 | D. | 649×106 |
 河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.
河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.
 如图,在△ABC中,AB=AC,∠A=108°,∠B的平分线交AC于点D,求证:DC+AB=BC.
如图,在△ABC中,AB=AC,∠A=108°,∠B的平分线交AC于点D,求证:DC+AB=BC.