题目内容
18.不等式组$\left\{\begin{array}{l}{3x+4≥0}\\{\frac{1}{2}x+\frac{2}{3}≤1}\end{array}\right.$的所有整数解的积为( )| A. | -1 | B. | 1 | C. | 0 | D. | -2 |
分析 先分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出符合条件的x的所有整数解相乘即可求解.
解答 解:$\left\{\begin{array}{l}{3x+4≥0①}\\{\frac{1}{2}x+\frac{2}{3}≤1②}\end{array}\right.$,
解不等式①得:x≥-$\frac{4}{3}$,
解不等式②得:x≤$\frac{2}{3}$,
则不等式组的解集为-$\frac{4}{3}$≤x≤$\frac{2}{3}$,
整数解为-1,0,
所以所有整数解的积为0,
故选C.
点评 本题考查的是解一元一次不等式组及求一元一次不等式组的整数解,求不等式组的公共解集,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.一元一次不等式x+1≥2的解在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
9.下列各运算中,正确的是( )
| A. | 30+3-3=-3 | B. | $\sqrt{5}-\sqrt{2}$=$\sqrt{3}$ | C. | (2a2)3=6a6 | D. | -a8÷a4=-a4 |
3.下列四个数中,比-2小的数是( )
| A. | -1 | B. | 0 | C. | -3 | D. | -$\frac{1}{2}$ |
8.为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
| A. | 5,5,$\frac{3}{2}$ | B. | 5,5,10 | C. | 6,5.5,$\frac{11}{6}$ | D. | 5,5,$\frac{5}{3}$ |

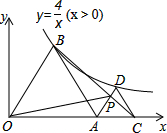 如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4.
如图,△AOB与△ACD均为正三角形,且顶点B、D均在双曲线y=$\frac{4}{x}$(x>0)上,点A、C在x轴上,连接BC交AD于点P,则△OBP的面积=4.