题目内容
1．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第6个图形需要黑色棋子的个数是48．
分析 由图可知：第1个图形需要黑色棋子的个数是2×3-3=3，第2个图形需要黑色棋子的个数是3×4-4=8，第3个图形需要黑色棋子的个数是4×5-5=15，…按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是（n+1）（n+2）-（n+2）=n2+2n．由此代入求得答案即可．
解答 解：∵第1个图形需要黑色棋子的个数是2×3-3=3，
第2个图形需要黑色棋子的个数是3×4-4=8，
第3个图形需要黑色棋子的个数是4×5-5=15，
…
∴第n个图形需要黑色棋子的个数是（n+1）（n+2）-（n+2）=n2+2n；
则第6个图形需要黑色棋子的个数是36+12=48，
故答案为：48．
点评 此题考查图形的变化规律，首先计算几个特殊图形，发现：数出每边上的个数，乘以边数再减去各个顶点的重复的点数，得出规律，解决问题．
练习册系列答案
相关题目
11．下列等式从左到右的变形正确的是（ ）
| A． | $\frac{b}{a}$=$\frac{bm}{am}$ | B． | $\frac{b}{a}$=$\frac{{b}^{3}}{a}$ | C． | $\frac{ab}{{a}^{2}}$=$\frac{b}{a}$ | D． | $\frac{ab-1}{ac-1}$=$\frac{b-1}{c-1}$ |
6．下列关系正确的是（ ）
| A． | （a+b）2=a2+b2 | B． | （a-b）2=a2-b2 | C． | （a+b）（a-b）=a2-b2 | D． | （a-b）2=a2-2ab-b2 |
13．去年12月，汉丰湖钓鱼比赛如期举行，其中8名选手某项得分如表：
则这8名选手得分的众数、中位数分别是（ ）
| 得分 | 80 | 85 | 87 | 90 |
| 人数 | 1 | 3 | 2 | 2 |
| A． | 85、85 | B． | 85、86 | C． | 85、87 | D． | 90、86 |
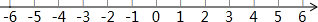解不等式组$\left\{\begin{array}{l}{x+1≤3}\\{x-1＜4（x+2）}\end{array}\right.$，并把解集在数轴上表示出来．