题目内容
7. 如图,圆锥的底面半径OB=6cm,高CO=8cm,则这个圆锥的侧面展开图的圆心角是( )
如图,圆锥的底面半径OB=6cm,高CO=8cm,则这个圆锥的侧面展开图的圆心角是( )| A. | 120° | B. | 180° | C. | 216° | D. | 236° |
分析 先根据勾股定理计算出母线长,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式求这个圆锥的侧面展开图的圆心角.
解答 解:圆锥的母线长=$\sqrt{{6}^{2}+{8}^{2}}$=10,
设这个圆锥的侧面展开图的圆心角为n°,
根据题意得2π•6=$\frac{n•π•10}{180}$,解得n=216,
即这个圆锥的侧面展开图的圆心角为216°.
故选C.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
18.如图,图①是一块边长为1,周长记为P1的等边三角形纸板,沿图①的底边剪去一块边长为$\frac{1}{2}$的等边三角形纸板后得到图②然后沿同一底边依次剪去一块更小的等边三角形纸板(即其边长为前一块被剪掉等边三角形纸板边长的$\frac{1}{2}$)后,得图③、④,…,记第n(n≥3)块纸板的周长为Pn,则Pn+1-Pn等于( )


| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | 3-$\frac{1}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n}}$-$\frac{1}{{2}^{n+1}}$ |
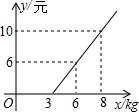 汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.
汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示. 如图,在平行四边形ABCD中,如果AE∥CF,那么BE与DF有怎样的数量关系?请说明理由.
如图,在平行四边形ABCD中,如果AE∥CF,那么BE与DF有怎样的数量关系?请说明理由.