题目内容
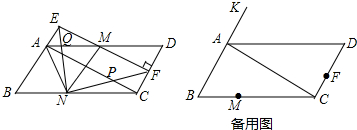
3.已知,如图,?ABCD中,BC=8cm,CD=4cm,∠B=60°,点E从点A出发,沿BA方向匀速运动,速度为1cm/s.过点E作EF⊥CD,垂足是F,连接EF交AD于点M,过M作MN∥AB,MN与BC交于点N,设运动时间为t(s)(0<t<4)(1)用含t的代数式表示线段AM的长:AM=2t;
(2)是否存在某一时刻t,使EN⊥BC,求出相应的t值,若不存在,说明理由;
(3)设四边形AEFN的面积为y(cm2),求y与t之间的函数关系式;
(4)点P是AC与NF的交点,在点E的运动过程中,是否存在某一时刻t,使∠MNP=45°?若存在,求出相应的t值,若不存在,说明理由.
分析 (1)在RT△AEM中,根据AM=2AE即可解决问题.
(2)在△OMN中,MN=4,∠NOM=90°,∠OMN=60°根据cos60°=$\frac{MO}{MN}$=$\frac{\frac{3}{2}t}{4}$=$\frac{1}{2}$即可解决问题.
(3)根据S四边形AEFN=S△AEM+S△AMN+S△MNF=$\frac{1}{2}$•AE•EM+$\frac{1}{2}$•AM•h+$\frac{1}{2}$•MN•MF即可解决.
(4)可以证明MN=MF,由此列出方程即可解决问题.
解答 解:(1)如图1中,∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠EAD=∠ABC=60°,
∵EF⊥CD,
∴EF⊥AB,
在RT△AME中,∵∠AEM=90°,AE=t,∠EMA=30°,
∴AM=2AE=2t,
故答案为2t.
(2)存在,如图1中,设AM交EN于点O,
∵EN⊥BC,
∴ENB=∠MON=∠AOE=90°,
在△AOE中,∠AOE=90°,∠EAB=60°,AE=t,
∴AO=$\frac{1}{2}$t,OM=$\frac{3}{2}$t,
∵MN∥AB,
易得MN=AB=4,且∠NMA=60°,
在△OMN中,MN=4,∠NOM=90°,∠OMN=60°,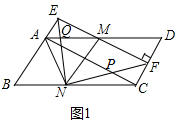
∴cos60°=$\frac{MO}{MN}$=$\frac{\frac{3}{2}t}{4}$=$\frac{1}{2}$.解得t=$\frac{4}{3}$;
(3)如图1中,由(1),(2)知AE=t,EM=$\sqrt{3}$t,AM=2t,AD与BC之间的距离h为2$\sqrt{3}$,MN=4,
在△MDF中,MD=8-2t,∠D=60°,
∴DF=4-t,MF=$\sqrt{3}$DF=$\sqrt{3}$(4-t),
∴S四边形AEFN=S△AEM+S△AMN+S△MNF=$\frac{1}{2}$•AE•EM+$\frac{1}{2}$•AM•h+$\frac{1}{2}$•MN•MF
=$\frac{1}{2}$•t•2t+$\frac{1}{2}$•2t•2$\sqrt{3}$+$\frac{1}{2}$•4•$\sqrt{3}$(4-t)
=$\frac{\sqrt{3}}{2}$t2+8$\sqrt{3}$,
∴y=$\frac{\sqrt{3}}{2}$t2+8$\sqrt{3}$(0<t<4).
(4)如图1中,∵∠MNP=45°,∠NMF=90°,
∴∠MNF=∠MFN=45°,
∴MN=MF,
∴4=$\sqrt{3}$(4-t),
∴t=4-$\frac{4\sqrt{3}}{3}$.
点评 本题考查四边形综合题、平行四边形的性质、30度角所对的直角边等于斜边一半、锐角三角函数等知识,解题的关键是熟练掌握特殊三角形边角之间的关系,学会分割法求面积,学会用方程的思想思考问题,属于中考压轴题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案| A. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y+1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{2x+3y=16}\\{x=y+1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{3x+2y=16}\\{x=y-1}\end{array}\right.$ |
| A. | $\sqrt{5}$,$\sqrt{12}$,$\sqrt{13}$ | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 3,4,5 | D. | 6,8,10 |
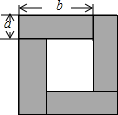 如图是用4个全等的长方形拼成一个“回形”正方形.
如图是用4个全等的长方形拼成一个“回形”正方形.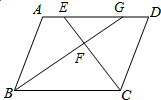 已知:如图,在?ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.
已知:如图,在?ABCD中,∠BCD的平分线CE交AD于点E,∠ABC的平分线BG交CE于点F,交AD于点G.
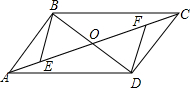 如图,?ABCD的对角线AC、BD相交于点O,OE=OF.
如图,?ABCD的对角线AC、BD相交于点O,OE=OF.