题目内容
5.有一组数能同时满足方程3x+2y=7和3x+2y=-6吗?此时方程组$\left\{\begin{array}{l}{3x+2y=7}\\{3x+2y=-6}\end{array}\right.$的解是什么情况?一次函数y=-$\frac{3}{2}$x+$\frac{7}{2}$与y=-$\frac{3}{2}$x-3的图象之间有什么位置关系?分析 由于7≠-6,则可判断没有一组数能同时满足方程3x+2y=7和3x+2y=-6,所以方程组$\left\{\begin{array}{l}{3x+2y=7}\\{3x+2y=-6}\end{array}\right.$无解,然后根据一次函数与一元二次方程组的关系可判断两函数图象平行.
解答 解:没有一组数能同时满足方程3x+2y=7和3x+2y=-6,此时方程组$\left\{\begin{array}{l}{3x+2y=7}\\{3x+2y=-6}\end{array}\right.$无解,
所以一次函数y=-$\frac{3}{2}$x+$\frac{7}{2}$与y=-$\frac{3}{2}$x-3的图象平行.
点评 本题主要考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
15.若a,b(a<b)是关于x的方程x-(x-m)(x-n)=0的两根,且m<0<n,则a,b,m,n的大小关系是( )
| A. | m<a<b<n | B. | a<m<n<b | C. | a<m<b<n | D. | m<a<n<b |
14.某人沿坡度为i=1:$\frac{\sqrt{3}}{3}$的山路行了40m,则该人升高了( )
| A. | 20$\sqrt{3}$m | B. | $\frac{20\sqrt{3}}{3}$m | C. | 10$\sqrt{3}$m | D. | $\frac{40}{3}$$\sqrt{3}$m |




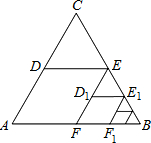 如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.
如图,△ABC是边长为1的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作S1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作S2.照此规律作下去,则S2015=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$.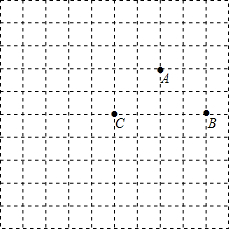 如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.
如图,网格中的每一个方格的边长都相等,点A,B,C都在网格的格点上,按要求完成下列各小题.