题目内容
18.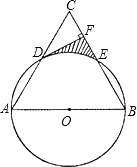 已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求图中阴影部分的面积.
分析 (1)连接DO,要证明DF为⊙O的切线只要证明∠FDP=90°即可;
(2)首先由已知可得到CD,CF的长,从而利用勾股定理可求得DF的长;再连接OE,求得CF,EF的长,从而利用S直角梯形FDOE-S扇形OED求得阴影部分的面积.
解答 解:
(1)证明:连接DO.
∵△ABC是等边三角形,
∴∠A=∠C=60°.
∵OA=OD,
∴△OAD是等边三角形.
∴∠ADO=60°,
∵DF⊥BC,
∴∠CDF=90°-∠C=30°,
∴∠FDO=180°-∠ADO-∠CDF=90°,
∴DF为⊙O的切线;
(2)∵△OAD是等边三角形,
∴AD=AO=$\frac{1}{2}$AB=2.
∴CD=AC-AD=2.
Rt△CDF中,
∵∠CDF=30°,
∴CF=$\frac{1}{2}$CD=1.
∴DF=$\sqrt{C{D}^{2}-C{F}^{2}}$,
连接OE,则CE=2.
∴CF=1,
∴EF=1.
∴S直角梯形FDOE=$\frac{1}{2}$(EF+OD)•DF=$\frac{3\sqrt{3}}{2}$,
∴S扇形OED=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,
∴S阴影=S直角梯形FDOE-S扇形OED=$\frac{3\sqrt{3}}{2}$-$\frac{2π}{3}$.
点评 此题考查学生对切线的判定及扇形的面积等知识点的掌握情况,当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了等边三角形的性质和利用割补法计算补规则图形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.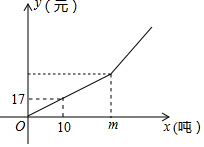 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
(1)求出m的值;
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
 为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:
为节约用水、保护水资源,本市制定了一套节约用水的管理措施,其中规定每月用水量超过m(吨)时,超过部分每吨加收环境保护费$\frac{m}{100}$元.下图反映了每月收取的水费y(元)与每月用水量x(吨)之间的函数关系的图象.按上述方案,一家酒店四、五两月用水量及缴费情况如表:| 月份 | 用水量x(吨) | 水费y(元) |
| 四月 | 35 | 59.5 |
| 五月 | 80 | 151 |
(2)写出y与x之间的函数关系式,并指出自变量x的取值范围.
8.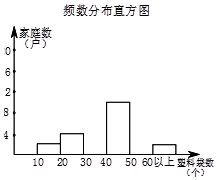 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
根据以上提供的信息,解答下列问题:
(1)补全频数分布表和频数分布直方图;
(2)请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有多少户?
 小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:
小明要统计小区500户居民每月丢弃塑料袋的数量情况,他随机调查了其中40户居民,按每月丢弃的塑料袋的数量分组进行统计,并绘制了如下的频数分布表和频数分布直方图:| 组别 | 每月丢塑料袋个数 | 频数 | 频率 |
| 第1组 | 10至19 | 2 | 0.05 |
| 第2组 | 20至29 | 4 | 0.10 |
| 第3组 | 30至39 | 6 | 0.15 |
| 第4组 | 40至49 | 10 | 0.25 |
| 第5组 | 50至59 | 16 | 0.40 |
| 第6组 | 60以上 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
(1)补全频数分布表和频数分布直方图;
(2)请你估算该小区每月丢弃塑料袋的数不少于40个的户数大约有多少户?
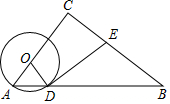 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E.
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,过点D作⊙O的切线交BC于点E. 如图,矩形ABCD的对角线AC、BD相交于点O,OA=3,则BD的长为6.
如图,矩形ABCD的对角线AC、BD相交于点O,OA=3,则BD的长为6.