题目内容
13.(1)解方程:x2-6x-5=0(2)解不等式组$\left\{\begin{array}{l}{2x-1>3x}\\{x-3≤\frac{1}{2}x-1}\end{array}\right.$.
分析 (1)移项,配方,开方,即可得出两个方程,求出方程的解即可;
(2)先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:(1)移项得:x2-6x=5,
配方得:x2-6x+9=5+9,
(x-3)2=14,
开方得:x-3=$±\sqrt{14}$,
x1=3+$\sqrt{14}$,x2=3-$\sqrt{14}$;
(2)$\left\{\begin{array}{l}{2x-1>3x①}\\{x-3≤\frac{1}{2}x-1②}\end{array}\right.$,
∵解不等式①得:x<-1,
解不等式②得:x≤4,
∴不等式组的解集为x<-1.
点评 本题考查了解一元二次方程,解一元一次不等式和解一元一次不等式组,能选择适当的方法解一元二次方程是解(1)的关键,能根据不等式的解集找出不等式组的解集是解(2)的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
3.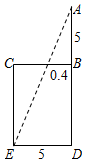 “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
 “今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )
“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学《九章算术》中的“井深几何”问题,它的题意可以由图获得,则井深为( )| A. | 1.25尺 | B. | 57.5尺 | C. | 6.25尺 | D. | 56.5尺 |
 有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.
有一个平分角的仪器如图所示,其中AB=AD,BC=DC.求证:AC平分∠BAD.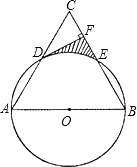 已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F. 如图,?ABCD中,AB=3,BC=5,∠ABC的平分线与AD相交于点E,求DE的长.
如图,?ABCD中,AB=3,BC=5,∠ABC的平分线与AD相交于点E,求DE的长.