题目内容
2. 如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为$\frac{8}{5}$.
如图,⊙O的直径AB=4,BC切⊙O于点B,OC平行于弦AD,OC=5,则AD的长为$\frac{8}{5}$.
分析 首先由切线的性质得出OB⊥BC,根据锐角三角函数的定义求出cos∠BOC的值;由直径所对的圆周角是直角,得出∠ADB=90°,又由平行线的性质知∠A=∠BOC,则cos∠A=cos∠BOC,在直角△ABD中,由余弦的定义求出AD的长.
解答 解:∵AB是直径,∴∠ADB=90°,
∵OC∥AD,
∴∠A=∠BOC,
∴cos∠A=cos∠BOC.
∵BC切⊙O于点B,
∴OB⊥BC,
∴cos∠BOC=$\frac{OB}{OC}$=$\frac{2}{5}$,
∴cos∠A=cos∠BOC=$\frac{2}{5}$.
又∵cos∠A=$\frac{AD}{AB}$,AB=4,
∴AD=$\frac{8}{5}$.
故答案为$\frac{8}{5}$
点评 本题综合考查切线、平行线、圆周角的性质,锐角三角函数的定义等知识点的运用.此题是一个综合题,难度中等.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
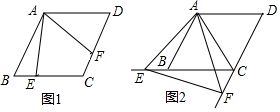
17.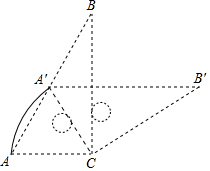 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )| A. | πcm | B. | 2πcm | C. | $\frac{8π}{3}cm$ | D. | 4πcm |