题目内容
网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大?
考点:二次函数的应用
专题:
分析:(1)设去年的售价为x元,则今年的售价为(1+50%)x元,去年的产量为y千克,则今年的产量为(y+2000)千克,根据条件建立方程组求出其解即可;
(2)由(1)的结论可以求出今年的产量,就可以求出日销售量,设日销售利润为W元,网上售价为a元,由利润问题的数量关系表示出W与a的数量关系,由二次函数的性质就可以求出结论.
(2)由(1)的结论可以求出今年的产量,就可以求出日销售量,设日销售利润为W元,网上售价为a元,由利润问题的数量关系表示出W与a的数量关系,由二次函数的性质就可以求出结论.
解答:解:(1)设去年的售价为x元,则今年的售价为(1+50%)x元,去年的产量为y千克,则今年的产量为(y+2000)千克,由题意,得
,
解得:
.
则今年的售价为(1+50%)x=9元.
答:去年的售价为6元,则今年的售价为9元;
(2)由题意,得
今年的产量为:10000+2000=12000千克,
则网上日销售量为:12000÷20=600千克.
设日销售利润为W元,网上售价为a元,由题意,得
W=a(600-
×5),
W=-50a2+1050a
W=-50(a-
)2+
,
∴a=-50<0,
∴a=
时,W最大=
.
∴网上售价定为10.5元,才能使日销量收入最大为
元.
|
解得:
|
则今年的售价为(1+50%)x=9元.
答:去年的售价为6元,则今年的售价为9元;
(2)由题意,得
今年的产量为:10000+2000=12000千克,
则网上日销售量为:12000÷20=600千克.
设日销售利润为W元,网上售价为a元,由题意,得
W=a(600-
| a-9 |
| 0.1 |
W=-50a2+1050a
W=-50(a-
| 21 |
| 2 |
| 11025 |
| 2 |
∴a=-50<0,
∴a=
| 21 |
| 2 |
| 11025 |
| 2 |
∴网上售价定为10.5元,才能使日销量收入最大为
| 11025 |
| 2 |
点评:本题考查了列二元二次方程组解实际问题的运用,二元二次方程组的解法的运用,二次函数的运用,二次函数的性质的运用,解答时求出二次函数的解析式是关键.

练习册系列答案
相关题目
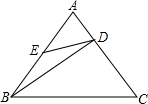 如图,正△ABC中,点E是AB的中点,点D在AC上,且DC=2DA,则( )
如图,正△ABC中,点E是AB的中点,点D在AC上,且DC=2DA,则( )| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
下列计算:①(-1)4=-1;②(-2)4=16;③(-3)3=-9;④-24=16.其中正确的是( )
| A、①②③④ | B、②③④ |
| C、②③ | D、② |
 如图,P为△ABC的边AB、AC的垂直平分线的交点,∠BAC=50°,求∠BPC的度数.
如图,P为△ABC的边AB、AC的垂直平分线的交点,∠BAC=50°,求∠BPC的度数.