题目内容
11.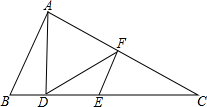 如图,△ABC中,AD⊥BC,∠B=2∠C,E,F分别是BC,AC的中点,若DE=3,求线段AB的长.
如图,△ABC中,AD⊥BC,∠B=2∠C,E,F分别是BC,AC的中点,若DE=3,求线段AB的长.
分析 作BH平分∠ABC交AC于H,连结HE,如图,由于∠B=2∠C,则∠CBH=∠C,于是可判断△HBC为等腰三角形,根据等腰三角形的性质得HE⊥BC,易得HE∥AD,根据平行线分线段成比例定理得$\frac{AH}{HC}$=$\frac{DE}{EC}$,接着根据角平分线的性质定理得$\frac{AH}{HC}$=$\frac{BA}{BC}$,则$\frac{DE}{EC}$=$\frac{BA}{BC}$,然后把BC=2EC代入计算即可得到AB=6.
解答 解:作BH平分∠ABC交AC于H,连结HE,如图,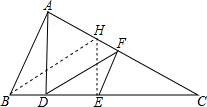
∵BH平分∠ABC,
∴∠CBH=$\frac{1}{2}$∠ABC,
∵∠B=2∠C,
∴∠CBH=∠C,
∴△HBC为等腰三角形,
∵点E为BC的中点,
∴HE⊥BC,
∵AD⊥BC,
∴HE∥AD,
∴$\frac{AH}{HC}$=$\frac{DE}{EC}$,
∵BH为∠ABC的平分线,
∴$\frac{AH}{HC}$=$\frac{BA}{BC}$,
∴$\frac{DE}{EC}$=$\frac{BA}{BC}$,即$\frac{3}{EC}$=$\frac{BA}{2EC}$,
∴AB=6.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.也考查了等腰三角形的判定与性质和角平分线性质.

练习册系列答案
相关题目
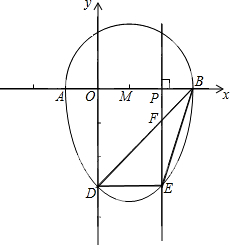 我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.
我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.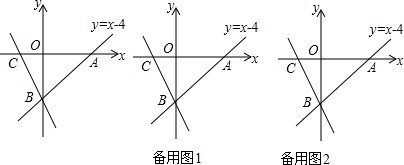
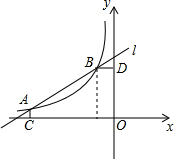 已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.
已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.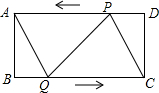 如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?
如图所示,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s,连接PQ、AQ、CP,设点P、Q运动的时间为t s.当t为何值时,四边形ABQP是矩形?