题目内容
6.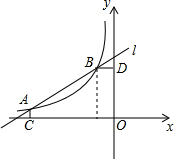 已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.
已知关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2满足x12=4-x22,反比例函数y=-$\frac{2k}{x}$的图象与直线l关于A(-4,m),B(-1,n)两点(如图),AC⊥x轴于C,BD⊥y轴于D.(1)求k的值以及直线l的解析式;
(2)P是线段AB上的一点(不与A、B重合),连接PC,PD,△PCA的面积记为S1,△PDB的面积记为S2.
①求证S1+S2为定值;
②求S1•S2的最大值,且求出此时点P的坐标.
分析 (1)根据根与系数的关系,可得关于k的方程,根据解方程,可得k值,根据自变量与函数值的对应关系,可得A、B点坐标,根据待定系数法,可得直线的解析式;
(2)根据图形割补法,可得S1,S2.
①根据等式的性质,可得答案;
②根据整式的乘法,可得二次函数,根据二次函数的增减性,可得答案.
解答 解:(1)由关于x的方程x2+2kx+k2-2k+1=0的两个实数根x1,x2,
得x1+x2=-2k,x1•x2=k2-2k+1.
由x1、x2满足x12=4-x22,得k2+2k-3=0.
解得k=3,k=-1(不符合题意舍去),
反比例函数的解析式为y=$\frac{-6}{x}$,
当x=-4时,y=$\frac{3}{2}$,即A(-4,$\frac{3}{2}$)
当x=-1时,y=6,即B(-1,6),
设直线AB的解析式为y=kx+b,
将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{-4b+k=\frac{3}{2}}\\{-k+b=6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=\frac{15}{2}}\end{array}\right.$.
故直线AB的解析式为y=$\frac{3}{2}$x+$\frac{15}{2}$;
(2)如图:
设P点坐标为(a,$\frac{3}{2}$a+$\frac{15}{2}$),
直线AB的解析式为y=$\frac{3}{2}$x+$\frac{15}{2}$,
当x=0时,y=$\frac{15}{2}$即E(0,$\frac{15}{2}$),
当y=0时,x=-5,即F(-5,0).
①证明:∵S1=S△PFC-S△AFC=$\frac{1}{2}$×1×($\frac{3}{2}$x+$\frac{15}{2}$)-$\frac{1}{2}$×1×$\frac{3}{2}$=$\frac{3}{4}$x+3,
S2=S△PDE-S△BDE=$\frac{1}{2}$×($\frac{15}{2}$-6)×(-1-x)=-$\frac{3}{4}$x-$\frac{3}{4}$,
∴S1+S2=$\frac{3}{4}$x+3+(-$\frac{3}{4}$x-$\frac{3}{4}$)=$\frac{9}{4}$,
∴S1+S2为定值;
②S1•S2=($\frac{3}{4}$x+3)(-$\frac{3}{4}$x-$\frac{3}{4}$)
=-$\frac{9}{16}$x2-$\frac{45}{16}$x-$\frac{9}{4}$
当x=-$\frac{5}{2}$时,S1•S2最大=$\frac{4×(-\frac{9}{4})×(-\frac{9}{16})-(-\frac{45}{16})^{2}}{4×(-\frac{9}{16})}$=$\frac{81}{64}$,
当x=-$\frac{5}{2}$时,$\frac{3}{2}$×(-$\frac{5}{2}$)+$\frac{15}{2}$=$\frac{15}{4}$,
P(-$\frac{5}{2}$,$\frac{15}{4}$)
点评 本题考查了反比例函数综合题,利用了根与系数的关系,自变量与函数值的对应关系,待定系数法求函数解析式;利用图形割补法是求面积的关键,又利用了二次函数的性质.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案| A. | m2+n2=(m+n)2 | B. | x2-1=x(x-$\frac{1}{x}$) | C. | a2-2a-1=(a-1)2-2 | D. | x2-4y2=(x-2y)(x+2y) |
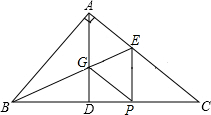 如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
如图,在Rt△ABC中,AD是高线,BE平分∠ABC交AC于E,交AD于G,过E作EP⊥BC于P,连接GP,请问四边形AGPE是什么四边形?为什么?
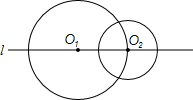 如图,半径为4的⊙O1的圆心O1在直线l上,半径为2的⊙O2的圆心O2既在直线l上,又在⊙O1上,⊙P的圆心P在直线l上,且⊙P与⊙O1、⊙O2都相切,则⊙P的半径为3或5.
如图,半径为4的⊙O1的圆心O1在直线l上,半径为2的⊙O2的圆心O2既在直线l上,又在⊙O1上,⊙P的圆心P在直线l上,且⊙P与⊙O1、⊙O2都相切,则⊙P的半径为3或5.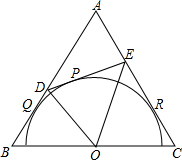 如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.
如图,在边长为a的等边△ABC中,半圆O的直径在BC上,又分别与AB、AC相切于点Q、R,点P是弧QR上(不包括Q、R点)任意一点,过点P的切线分别与AB、AC相交于点D、E.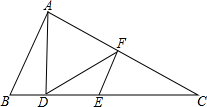 如图,△ABC中,AD⊥BC,∠B=2∠C,E,F分别是BC,AC的中点,若DE=3,求线段AB的长.
如图,△ABC中,AD⊥BC,∠B=2∠C,E,F分别是BC,AC的中点,若DE=3,求线段AB的长. 如图,∠GEF和∠DFE的角平分线相交于点H,AB∥CD,∠B=∠D,求证:EH⊥HF.
如图,∠GEF和∠DFE的角平分线相交于点H,AB∥CD,∠B=∠D,求证:EH⊥HF.