题目内容
17.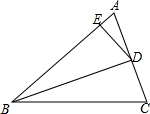 已知如图,在△ABC中,BD平分∠ABC交AC于点D,点E在AB上,且BD2=BE•BC;
已知如图,在△ABC中,BD平分∠ABC交AC于点D,点E在AB上,且BD2=BE•BC;(1)求证:∠BDE=∠C;
(2)求证:AD2=AE•AB.
分析 (1)根据角平分线的定义得到∠ABD=∠CBD,由BD2=BE•BC,得到$\frac{BD}{BE}=\frac{BC}{BD}$,推出△EBD∽△DBC,根据相似三角形的性质即可得到结论;
(2)由∠BDE=∠C,推出∠DBC=∠ADE,等量代换得到∠ABD=∠ADE,证得△ADE∽△ABD,根据相似三角形的性质即可得到结论.
解答 证明:(1)∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵BD2=BE•BC,
∴$\frac{BD}{BE}=\frac{BC}{BD}$,
∴△EBD∽△DBC,
∴∠BDE=∠C;
(2)∵∠BDE=∠C,
∠DBC+∠C=∠BDE+∠ADE,
∴∠DBC=∠ADE,
∵∠ABD=∠CBD,
∴∠ABD=∠ADE,
∴△ADE∽△ABD,
∴$\frac{AD}{AB}=\frac{AE}{AD}$,
即AD2=AE•AB.
点评 本题考查了相似三角形的判定和性质,角平分线的性质,熟练掌握相似三角形的性质即可得到结论.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知两圆的半径分别是3和5,圆心距是1,那么这两圆的位置关系是( )
| A. | 内切 | B. | 外切 | C. | 相交 | D. | 内含 |
9. 某月份的日历表如图.任意圈出一横行或一竖列相邻的三个数.这三个数的和不可能是( )
某月份的日历表如图.任意圈出一横行或一竖列相邻的三个数.这三个数的和不可能是( )
 某月份的日历表如图.任意圈出一横行或一竖列相邻的三个数.这三个数的和不可能是( )
某月份的日历表如图.任意圈出一横行或一竖列相邻的三个数.这三个数的和不可能是( )| A. | 24 | B. | 42 | C. | 58 | D. | 66 |
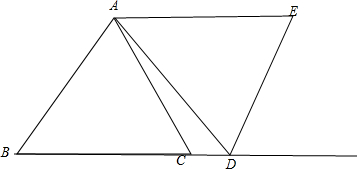 如图,△ABC与△ADE都是等边三角形,点D在直线BC的延长线上,连接CE,试猜想AB与CE的位置关系并说明理由.
如图,△ABC与△ADE都是等边三角形,点D在直线BC的延长线上,连接CE,试猜想AB与CE的位置关系并说明理由.