题目内容
A、B两车分别从相距40km的甲、乙两地同向而行(A车在B车后),A车在B车出发1h后才出发,结果A车用了3h与B车同时到达目的地,已知A车的速度是B车的
倍,A车的速度为 ,B车的速度为 .
| 3 |
| 2 |
考点:一元一次方程的应用
专题:
分析:设B车的速度为xkm/h,表示出A车的速度为
xkm/h,然后根据A车行驶的路程减去B车行驶的路程等于甲乙两地间的距离列出方程求解即可.
| 3 |
| 2 |
解答:解:设B车的速度为xkm/h,表示出A车的速度为
xkm/h,
由题意得,
x×3-(3+1)x=40,
解得x=80,
所以,
x=
×80=120km/h.
所以,A车的速度是120km/h,B车的速度是80km/h.
故答案为:120km/h;80km/h.
| 3 |
| 2 |
由题意得,
| 3 |
| 2 |
解得x=80,
所以,
| 3 |
| 2 |
| 3 |
| 2 |
所以,A车的速度是120km/h,B车的速度是80km/h.
故答案为:120km/h;80km/h.
点评:本题考查了一元一次方程的应用,读懂题目信息,找出追及问题的等量关系,然后列出方程是解题的关键,要注意两车行驶的时间不相等.

练习册系列答案
相关题目
把二次函数y=-
x2-x+3用配方法化成y=a(x-h)2+k的形式时,应为( )
| 1 |
| 4 |
A、y=-
| ||||
B、y=-
| ||||
C、y=-
| ||||
D、y=-(
|
 如图所示,已知在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交AB于E,交BC于F,BF=5cm,求FC.
如图所示,已知在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,交AB于E,交BC于F,BF=5cm,求FC.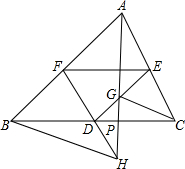 如图,设点D、E、F分别是△ABC三边的中点,过A作一直线与DE,FD分别交于G,H,求证:CG∥BH.
如图,设点D、E、F分别是△ABC三边的中点,过A作一直线与DE,FD分别交于G,H,求证:CG∥BH. 如图,AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠DAB=∠EAC
如图,AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠DAB=∠EAC