Question

12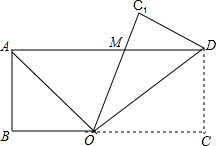．如图，在矩形纸片ABCD中，AB=1，AD=$\sqrt{3}$+1，∠BAD的平分线交BC于点O，将△DOC沿OD边对折得到△DOC₁，且OC₁交AD于点M．
（1）直接写出折痕OD的长为2，∠DOC=30度；
（2）试求出△ODM的周长；
（3）将△ODM绕点O逆时针旋转α角，得到△OD₁M₁，使得M的对应点M₁落在OA边上，请你在图中画出△OD₁M₁，并求出DM在旋转过程中所扫过的面积．

Answer 1

分析 （1）由四边形ABCD是矩形和角平分线的定义得到△ABO是等腰直角三角形，求得BO=AB=1，根据勾股定理得到OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=2，由三角函数的定义即可得到结论；
（2）根据折叠的性质得到∠MOD=∠COD=30°，DC₁=DC=1，∠C₁=∠C=90°，推出DM=OM，解直角三角形得到DM=OM=$\frac{\sqrt{3}}{2}$，于是得到结果；
（3）如图所示根据平角的定义得到∠M₁OM=180°-45°-60°=75°，根据扇形的面积公式即可得到结论．

解答 解：（1）∵四边形ABCD是矩形，
∴∠BAD=∠B=∠C=90°，BC=AD═$\sqrt{3}+1$，CD=AB=1，
∵AO平分∠BAD，
∴△ABO是等腰直角三角形，
∴BO=AB=1，
∴OC=$\sqrt{3}$，
∴OD=$\sqrt{O{C}^{2}+C{D}^{2}}$=2，
∵sin∠DOC=$\frac{CD}{OD}$=$\frac{1}{2}$，
∴∠DOC=30°，
故答案为：2，30；

（2）∵将△DOC沿OD边对折得到△DOC₁，
∴∠MOD=∠COD=30°，DC₁=DC=1，∠C₁=∠C=90°，
∵AD∥BC，
∴∠MDO=∠DOC=30°，
∴∠MOD=∠MDO=30°，
∴DM=OM，
∴∠C₁MD=60°，
∴DM=OM=$\frac{\sqrt{3}}{2}$，
∴△ODM的周长=DM+OM+OD=2+$\sqrt{3}$；

（3）如图所示，∵∠AOB=45°，∠C₁OC=60°，
∴∠M₁OM=180°-45°-60°=75°，
∴DM在旋转过程中所扫过的面积=S${\;}_{扇形OD{D}_{1}}$-S${\;}_{扇形OM{M}_{1}}$=$\frac{75•π×{2}^{2}}{360}$-$\frac{75•π×（\frac{\sqrt{3}}{2}）^{2}}{360}$=$\frac{95}{96}$π．

点评 本题考查了矩形的性质，折叠的性质，旋转的性质，扇形的面积的计算，正确的作出图形是解题的关键．