题目内容
16.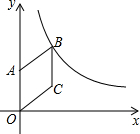 如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )
如图,在平面直角坐标系中,菱形OABC的顶点A在y轴的正半轴上,点B在函数y=$\frac{k}{x}$(x>0)的图象上,若点C的坐标为(4,3),则k的值为( )| A. | 12 | B. | 20 | C. | 24 | D. | 32 |
分析 延长BC交x轴于D,则BD⊥OD,根据菱形的性质以及勾股定理得出BC=OC=OA=5,即可得出B点坐标,进而求出k的值即可.
解答 解:延长BC交x轴于D,如图所示:
则BD⊥OD,
∵C的坐标为(4,3),
∴OD=4,CD=3,
∴OC=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵四边形OABC是菱形,
∴BC=OA=OC=5,
∴BD=5+3=8,
∴点B的坐标为(4,8),
把B(4,8)代入函数y=$\frac{k}{x}$(x>0)得:k=4×8=32;
故选:D.
点评 此题主要考查了菱形的性质、勾股定理和反比例函数图象上点的坐标性质;得出B点坐标是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在实数-3、0、5、$\sqrt{5}$中,最小的实数是( )
| A. | -3 | B. | 0 | C. | 5 | D. | $\sqrt{5}$ |
7. 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
 有一种圆柱体茶叶筒如图所示,则它的俯视图是( )
有一种圆柱体茶叶筒如图所示,则它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
11.已知点A(1,2)在反比例函数y=$\frac{k}{x}$的图象上,则该反比例函数的解析式是( )
| A. | y=$\frac{1}{x}$ | B. | y=$\frac{4}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=2x |
8.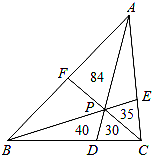 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
 如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )
如图,P为△ABC内一点,连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F,则把△ABC分成六个小三角形,其中四个小三角形面积已在图上标明,则△ABC的面积为( )| A. | 300 | B. | 315 | C. | 279 | D. | 342 |
5.在实数-2,6,0,1中,最小的实数是( )
| A. | -2 | B. | 6 | C. | 0 | D. | 1 |
 如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形.
如图,延长?ABCD的边AB到点E,使BE=BC,延长CD到点F,使DF=DA,连结AF,CE,求证:四边形AECF是平行四边形. 如图,已知△ABC,按如下步骤作图:
如图,已知△ABC,按如下步骤作图: