题目内容
1.已知一元二次方程:①x2-2x-3=0,②x2+2x+3=0.下列说法正确的是( )| A. | ①②都有实数解 | B. | ①无实数解,②有实数解 | ||
| C. | ①有实数解,②无实数解 | D. | ①②都无实数解 |
分析 分别找出两个一元二次方程的a、b和c的值,并代入△=b2-4ac,然后计算△,最后根据计算结果判断方程根的情况.
解答 解:①∵a=1,b=-2,c=-3,
∴△=b2-4ac=(-2)2-4×1×(-3)=16>0,
∴方程x2-2x-3=0有两个不相等的实数根;
②:∵a=1,b=2,c=3,
∴△=b2-4ac=22-4×1×3=-8<0,
∴方程x2+2x+3=0没有实数根;
故选C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的根的判别式△=b2-4ac.当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
相关题目
11.如图1,四边形ABCD、AEFG都是正方形,连接DE、BG.
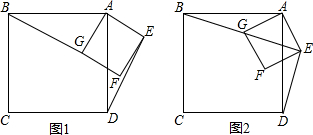
(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.

(1)求证:DE=BG;
(2)在图(2)中,连接GE,若点B、G、E在同一直线上时,AB=$\sqrt{3}$,DE=1,求AE的长.
6.方程x2-4x-3=0根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
10.-42的意义是( )
| A. | 2个-4相乘 | B. | 2个-4相加 | C. | 42的相反数 | D. | -4乘以2 |