题目内容
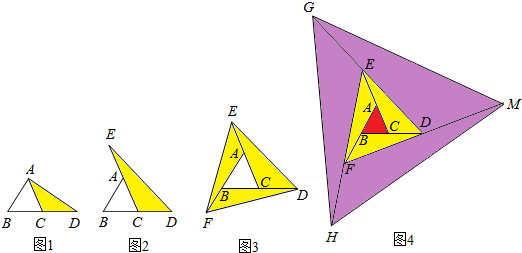
20.在图1到图4中,已知△ABC的面积为m.(1)如图1,延长△ABC的边BC到点D使CD=BC,连接DA,若△ACD的面积为S1,则S1=m.(用含m的式子表示)
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2=2m.(用含a的代数式表示)
(3)如图3,在图2的基础上延长AB到点F,使BF=AB,连接FD于E,得到△DEF,若阴影部分的面积为S3,则S3=6m.(用含a的代数式表示)
(4)可以发现将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF,如图3,此时,我们称△ABC向外扩展了一次.可以发现扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
(5)应用上面的结论解答下面问题:
去年在面积为15平方面的△ABC空地上栽种了各种花卉,今年准备扩大种植规模,把△ABC内外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH,如图4,求这两次扩展的区域(即阴影部分)面积共为多少平方米?
分析 (1)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(2)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(3)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(4)利用三角形的面积公式,等底同高的三角形面积相等,本题得以解决.
(5)根据第四问的经验,得出扩展一次面积变为原来的7倍,得出两次扩展面积,本题得以解决.
解答 解:(1)∵CD=BC,
∴△ABC和△ACD的面积相等(等底同高),
故得出结论S1=m.
(2)连接AD, ,
,
∵AE=CA,
∴△DEC的面积S2为△ACD的面积S1的2倍,
故得出结论S2=2m.
(3)结合(1)(2)得出阴影部分的面积为△DEC面积的3倍,
故得出结论则S3=6m.
(4)S△DEF=S阴影+S△ABC
=S3+S△ABC
=6m+m
=7m
=7S△ABC
故得出结论扩展一次后得到的△DEF的面积是原来△ABC面积的7倍.
(5)根据(4)结论可得两次扩展的区域(即阴影部分)面积共为(7×7-1)×15=720(平方米),
答:求这两次扩展的区域(即阴影部分)面积共为720平方米.
点评 本题考查了学生对面积公式的应用,同时考查到了学生的读题能力,利用类推的方法得出结论.解题的关键是找到扩展后的三角形的面积是原来的7倍.

练习册系列答案
相关题目
15.下列长度的三条线段,能组成三角形的是( )
| A. | 4,12,6 | B. | 3,8,4 | C. | 13,20,8 | D. | 9,17,8 |
5.下列图形中不是轴对称图形的是( )
| A. | 线段 | B. | 角 | ||
| C. | 含30°的直角三角形 | D. | 等腰直角三角形 |
 如图,四边形ABCD中,∠C=40°,∠B=∠D=90°,E、F分别是BC、DC上的一点,当△AEF的周长最小时,∠EAF的度数为100°.
如图,四边形ABCD中,∠C=40°,∠B=∠D=90°,E、F分别是BC、DC上的一点,当△AEF的周长最小时,∠EAF的度数为100°.
 为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题:
为了了解学生关注热点新闻的情况,“两会”期间,小明对班级同学一周内收看“两会”新闻的次数情况作了调查,调查结果统计如图所示(其中男生收看3次的人数没有标出).根据上述信息,解答下列各题: